题目内容
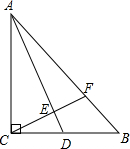 如图,已知在△ABC中,∠ACB=90°,AC=BC,AD是BC边上的中线,CE⊥AD于E,CE延长线交AB于F.求:
如图,已知在△ABC中,∠ACB=90°,AC=BC,AD是BC边上的中线,CE⊥AD于E,CE延长线交AB于F.求:(1)
| AE |
| DE |
(2)tan∠BAD的值.
考点:相似三角形的判定与性质,解直角三角形
专题:
分析:(1)由条件可证得△CED∽△AEC,可得到
=
=2;
(2)过D作DG⊥AB于点G,设BD=a,则BC=AC=2a,AB=2
a,利用面积相等可求得DG,且DG=BG,可求得AG,可求得∠BAD的正切值.
| AE |
| DE |
| AC |
| CD |
(2)过D作DG⊥AB于点G,设BD=a,则BC=AC=2a,AB=2
| 2 |
解答:解:
(1)∵∠ACB=90°,CE⊥AD,
∴∠AEC=∠ACD=90°,
∴∠ECD+∠EDC=∠CAE+∠EDC=90°,
∴∠ECD=∠CAE,
∴△AEC∽△CED,
∵D为BC中点,
∴AC=2CD,
∴
=
=2;
(2)过D作DG⊥AB于点G,设BD=a,则BC=AC=2a,AB=2
a,
∵BD=CD,
∴S△ACD=S△ABD,
∴AC•CD=AB•DG,即2a•a=2
a•DG,
∴DG=BG=
a,
∴AG=AB-BG=2
a-
a=
a,
∴tan∠BAD=
=
=
.
(1)∵∠ACB=90°,CE⊥AD,
∴∠AEC=∠ACD=90°,
∴∠ECD+∠EDC=∠CAE+∠EDC=90°,
∴∠ECD=∠CAE,
∴△AEC∽△CED,
∵D为BC中点,
∴AC=2CD,
∴
| AE |
| DE |
| AC |
| CD |
(2)过D作DG⊥AB于点G,设BD=a,则BC=AC=2a,AB=2
| 2 |
∵BD=CD,
∴S△ACD=S△ABD,
∴AC•CD=AB•DG,即2a•a=2
| 2 |
∴DG=BG=
| ||
| 2 |
∴AG=AB-BG=2
| 2 |
| ||
| 2 |
3
| ||
| 2 |
∴tan∠BAD=
| DG |
| AG |
| ||||
|
| 1 |
| 3 |
点评:本题主要考查相似三角形的判定和性质,掌握相似三角形的判定方法是解题的关键,注意方程思想和等积法的应用.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
观察下列图形,其中相似图形有( )


| A、1对 | B、2对 | C、3对 | D、4对 |
 如图,△ABC中,DE∥BC,EF∥AB,AD:BD=3:2,FC=2,AC=6,求DE和CE的长.
如图,△ABC中,DE∥BC,EF∥AB,AD:BD=3:2,FC=2,AC=6,求DE和CE的长.