题目内容
根据下列条件,分别求二次函数的表达式
(1)已知图象的顶点坐标为(-1,-8),且过点(0,-6);
(2)已知图象经过点(3,0),(2,-3),并以直线x=0为的对称轴.
(1)已知图象的顶点坐标为(-1,-8),且过点(0,-6);
(2)已知图象经过点(3,0),(2,-3),并以直线x=0为的对称轴.
考点:待定系数法求二次函数解析式
专题:计算题
分析:(1)根据顶点坐标设出抛物线顶点式,把(0,-6)代入求出a的值,即可确定出解析式;
(2)根据抛物线以直线x=0为对称轴,设出抛物线解析式,把已知两点坐标代入求出a与c的值,即可求出解析式.
(2)根据抛物线以直线x=0为对称轴,设出抛物线解析式,把已知两点坐标代入求出a与c的值,即可求出解析式.
解答:解:(1)设抛物线解析式为y=a(x+1)2-8,
把(0,-6)代入得:-6=a-8,即a=2,
则二次函数解析式为y=2(x+1)2-8=2x2+4x-6;
(2)根据题意设抛物线解析式为y=ax2+c,
把(3,0)与(2,-3)代入得:
,
解得:a=
,c=-
,
则抛物线解析式为y=
x2-
.
把(0,-6)代入得:-6=a-8,即a=2,
则二次函数解析式为y=2(x+1)2-8=2x2+4x-6;
(2)根据题意设抛物线解析式为y=ax2+c,
把(3,0)与(2,-3)代入得:
|
解得:a=
| 3 |
| 5 |
| 27 |
| 5 |
则抛物线解析式为y=
| 3 |
| 5 |
| 27 |
| 5 |
点评:此题考查了待定系数法求二次函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
观察下列图形,其中相似图形有( )


| A、1对 | B、2对 | C、3对 | D、4对 |
已知关于x的一元二次方程x2-(2k+1)x+k2+2k=0有两个实数根x1,x2,使x1•x2-x12-x22≥0成立,则k的值为( )
| A、-1 | B、1 |
| C、大于等于1 | D、不存在 |
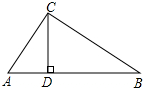 如图,△ABC中,∠ACB=90°,CD是高,若AB=13cm,AC=5cm,求CD的长.
如图,△ABC中,∠ACB=90°,CD是高,若AB=13cm,AC=5cm,求CD的长. 如图,△ABC中,DE∥BC,EF∥AB,AD:BD=3:2,FC=2,AC=6,求DE和CE的长.
如图,△ABC中,DE∥BC,EF∥AB,AD:BD=3:2,FC=2,AC=6,求DE和CE的长.