题目内容
20.先化简分式($\frac{x}{x-1}$-$\frac{x}{{x}^{2}-1}$)÷$\frac{{x}^{3}-x}{{x}^{2}-2x+1}$,若该分式的值等于$\frac{2}{3}$,求相应的x的值.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,使其值为$\frac{2}{3}$列出方程,求出方程的解即可得到x的值.
解答 解:原式=$\frac{x(x+1)-x}{(x+1)(x-1)}$•$\frac{(x-1)^{2}}{x(x+1)(x-1)}$=$\frac{{x}^{2}}{(x+1)(x-1)}$•$\frac{x-1}{x(x+1)}$=$\frac{x}{(x+1)^{2}}$,
根据题意得:$\frac{x}{(x+1)^{2}}$=$\frac{2}{3}$,
去分母得:2x2+4x+2=3x,即2x2+x+2=0,
此方程无解,
则x的值无解.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
11.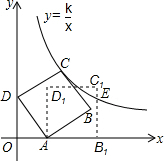 如图,在平面直角坐标系中,边长为5的正方形ABCD斜靠在y轴上,顶点A(3,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,得正方形AB1C1D1,且B1恰好落在x轴的正半轴上,此时边B1C1交反比例图象于点E,则点E的纵坐标是( )
如图,在平面直角坐标系中,边长为5的正方形ABCD斜靠在y轴上,顶点A(3,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,得正方形AB1C1D1,且B1恰好落在x轴的正半轴上,此时边B1C1交反比例图象于点E,则点E的纵坐标是( )
 如图,在平面直角坐标系中,边长为5的正方形ABCD斜靠在y轴上,顶点A(3,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,得正方形AB1C1D1,且B1恰好落在x轴的正半轴上,此时边B1C1交反比例图象于点E,则点E的纵坐标是( )
如图,在平面直角坐标系中,边长为5的正方形ABCD斜靠在y轴上,顶点A(3,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,得正方形AB1C1D1,且B1恰好落在x轴的正半轴上,此时边B1C1交反比例图象于点E,则点E的纵坐标是( )| A. | $\frac{5}{2}$ | B. | 3 | C. | $\frac{7}{2}$ | D. | 4 |
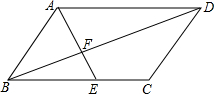 如图,在?ABCD中,点E为边BC的黄金分割点(BE>EC),AE与BD相交于点F,求$\frac{EC}{AD}$的值.
如图,在?ABCD中,点E为边BC的黄金分割点(BE>EC),AE与BD相交于点F,求$\frac{EC}{AD}$的值.