题目内容
5.已知关于x的不等式组$\left\{\begin{array}{l}{2x-3a<0}\\{3x+2a>0}\end{array}\right.$有三个整数解,求a的取值范围.分析 首先确定不等式组的解集,先利用含a的式子表示,根据整数解的个数就可以确定有哪些整数解,根据解的情况可以得到关于a的不等式,从而求出a的范围.
解答 解:$\left\{\begin{array}{l}{2x-3a<0①}\\{3x+2a>0②}\end{array}\right.$
∵解不等式①得:x<1.5a,
解不等式②得:x>-$\frac{2}{3}$a,
∴不等式组的解集为-$\frac{2}{3}$a<x<1.5a,
由于不等式组有解,则-$\frac{2}{3}$a<x≤$\frac{3}{2}$a,必定有整数解0,
∵|$\frac{3}{2}$a|>|-$\frac{2}{3}$a|,
∴三个整数解不可能是-2,-1,0.
若三个整数解为-1,0,1,则$\left\{\begin{array}{l}{1≤\frac{3}{2}a<2}\\{-2≤-\frac{2}{3}a<-1}\end{array}\right.$,此不等式组无解;
若三个整数解为0,1,2,则$\left\{\begin{array}{l}{2≤\frac{3}{2}a<3}\\{-1≤-\frac{2}{3}a<0}\end{array}\right.$,解得$\frac{4}{3}$≤a≤$\frac{3}{2}$,
所以a的取值范围是$\frac{4}{3}$≤a≤$\frac{3}{2}$.
点评 考查不等式组的解法及整数解的确定.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.本题要根据整数解的取值情况分情况讨论结果,取出合理的答案.

练习册系列答案
相关题目
17.现有A、B两个大小一样、质地均匀的小正方体(正方体的每个面上分别标有数字1,2,3,4,5,6),用娜娜抛掷A正方体朝上的数字为x,用莉莉抛掷B正方体朝上的数字为y,且点M的坐标为(x,y),则她们各投掷一次后,点M在一次函数y=-x+4的图象上的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{12}$ |
14.不等式组$\left\{\begin{array}{l}{2x-1>0}\\{x+5≥4}\end{array}\right.$的解集是( )
| A. | x>$\frac{1}{2}$ | B. | -1≤x<$\frac{1}{2}$ | C. | x<$\frac{1}{2}$ | D. | x≥-1 |
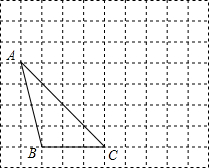 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,将△ABC先向右平移5个单位得△A1B1C1,再向上平移2个单位得△A2B2C2.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,将△ABC先向右平移5个单位得△A1B1C1,再向上平移2个单位得△A2B2C2.
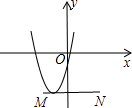 如图,线段MN在平面直角坐标系中,点M,N的坐标分别为(-2,-4),(3,-4),抛物线y=ax2+bx+c(a>0)顶点在线段MN上运动,该抛物线与x轴交于点C,D(点C在点D的左侧),下列结论中:①c≥-3;②当x>4时,y随x的增大而增大;③若点C的横坐标的最小值为-4,则点D的横坐标最小值为0,其中正确的有( )
如图,线段MN在平面直角坐标系中,点M,N的坐标分别为(-2,-4),(3,-4),抛物线y=ax2+bx+c(a>0)顶点在线段MN上运动,该抛物线与x轴交于点C,D(点C在点D的左侧),下列结论中:①c≥-3;②当x>4时,y随x的增大而增大;③若点C的横坐标的最小值为-4,则点D的横坐标最小值为0,其中正确的有( )