题目内容
10．
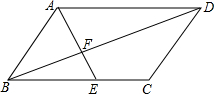如图，在?ABCD中，点E为边BC的黄金分割点（BE＞EC），AE与BD相交于点F，求$\frac{EC}{AD}$的值．
分析 由平行四边形的性质可得BC=AD，再根据点E是边BC上的黄金分割点，得出BE：BC的值，再求出$\frac{EC}{BC}$的值，等量代换即可求出结果．
解答 解：∵四边形ABCD是平行四边形，
∴BC=AD，
∵点E为边BC的黄金分割点（BE＞EC），
∴BE：BC=$\frac{\sqrt{5}-1}{2}$，即BE=$\frac{\sqrt{5}-1}{2}$BC，
∴EC=BC-BE=$\frac{3-\sqrt{5}}{2}$BC，
∴$\frac{EC}{BC}$=$\frac{3-\sqrt{5}}{2}$，
∴$\frac{EC}{AD}$=$\frac{3-\sqrt{5}}{2}$．
点评 本题考查了黄金分割：把一条线段分成两部分，使其中较长的线段为全线段与较短线段的比例中项，这样的线段分割叫做黄金分割，他们的比值（$\frac{\sqrt{5}-1}{2}$）叫做黄金比．也考查了平行四边形对边相等的性质．
练习册系列答案
相关题目
在△ABC中，中线AD、BE相交于点O，若△BOD的面积等于5，求△ABC的面积．
5．已知A组有三个数：1，-2，3，B组有三个数：1，-$\sqrt{2}$，$\sqrt{3}$，若从B组任选两个数分别与A组的每个数相乘，共得到6个数，再把这6个数相加得到数m，则m＞0的概率为（ ）
| A． | 0 | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | 1 |
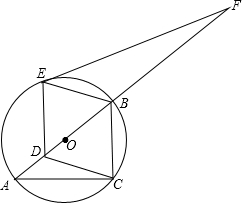如图，点A，B，C在⊙O上，AB是⊙O的直径，AC=4，BC=3．
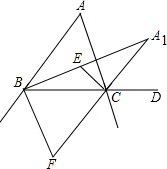如图，在△ABC中，点E是∠ABC、∠ACB角平分线的交点，点F是∠ABC、∠ACB外角平分线的交点，点A1是内角∠ABC、外角∠ACD平分线的交点．