题目内容
9.若关于x的不等式组$\left\{\begin{array}{l}{2x≥2}\\{\frac{a+2x}{3}>x}\end{array}\right.$无解,则a的取值范围是( )| A. | a<1 | B. | a≤1 | C. | a>1 | D. | a≥1 |
分析 首先计算出两个不等式的解集,再根据大大小小找不到可得a≤1.
解答 解:$\left\{\begin{array}{l}{2x≥2①}\\{\frac{a+2x}{3}>x②}\end{array}\right.$,
由①得:x≥1,
由②得:x<a,
∵不等式组无解,
∴a≤1,
故选:B.
点评 此题主要考查了解一元一次不等式组,关键是掌握解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
相关题目
17.现有A、B两个大小一样、质地均匀的小正方体(正方体的每个面上分别标有数字1,2,3,4,5,6),用娜娜抛掷A正方体朝上的数字为x,用莉莉抛掷B正方体朝上的数字为y,且点M的坐标为(x,y),则她们各投掷一次后,点M在一次函数y=-x+4的图象上的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{12}$ |
14.不等式组$\left\{\begin{array}{l}{2x-1>0}\\{x+5≥4}\end{array}\right.$的解集是( )
| A. | x>$\frac{1}{2}$ | B. | -1≤x<$\frac{1}{2}$ | C. | x<$\frac{1}{2}$ | D. | x≥-1 |
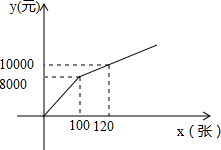 为丰富群众的业余生活,我市准备组织篮球比赛,市体育局策划本次活动,在与单位协商团购票时推出两种方案.设购买门票数为x(张),总费用为y(元).方案一:若单位赞助广告费8000元,则该单位所购门票的价格为每张50元;(总费用=广告赞助费+门票费)
为丰富群众的业余生活,我市准备组织篮球比赛,市体育局策划本次活动,在与单位协商团购票时推出两种方案.设购买门票数为x(张),总费用为y(元).方案一:若单位赞助广告费8000元,则该单位所购门票的价格为每张50元;(总费用=广告赞助费+门票费) 在△ABC中,中线AD、BE相交于点O,若△BOD的面积等于5,求△ABC的面积.
在△ABC中,中线AD、BE相交于点O,若△BOD的面积等于5,求△ABC的面积.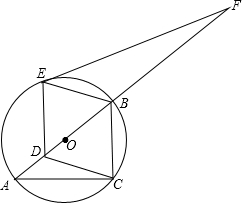 如图,点A,B,C在⊙O上,AB是⊙O的直径,AC=4,BC=3.
如图,点A,B,C在⊙O上,AB是⊙O的直径,AC=4,BC=3.