题目内容
11.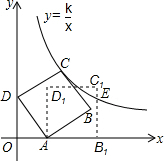 如图,在平面直角坐标系中,边长为5的正方形ABCD斜靠在y轴上,顶点A(3,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,得正方形AB1C1D1,且B1恰好落在x轴的正半轴上,此时边B1C1交反比例图象于点E,则点E的纵坐标是( )
如图,在平面直角坐标系中,边长为5的正方形ABCD斜靠在y轴上,顶点A(3,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,得正方形AB1C1D1,且B1恰好落在x轴的正半轴上,此时边B1C1交反比例图象于点E,则点E的纵坐标是( )| A. | $\frac{5}{2}$ | B. | 3 | C. | $\frac{7}{2}$ | D. | 4 |
分析 先根据勾股定理求出OD的长,再过点C作CF⊥y轴于点F,根据ASA定理得出△CDF≌△DAO,故可得出C点坐标,求出k的值,再求出OH的长,进而可得出E点坐标.
解答 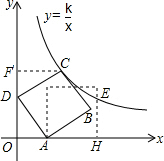 解:∵Rt△AOD中,OA=3,AD=5,
解:∵Rt△AOD中,OA=3,AD=5,
∴OD=$\sqrt{{AD}^{2}-{OA}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4.
过点C作CF⊥y轴于点F,
∵∠CDF+∠ADO=90°,∠CDF+∠DCF=90°,
∴∠DCF=∠ADO,
同理,∠CDF=∠DAO,
在△CDF与△DAO中,
$\left\{\begin{array}{l}∠DCF=∠ADO\\ CD=AD\\∠CDF=∠DAO\end{array}\right.$,
∴△CDF≌△DAO(ASA),
∴CF=OD=4,DF=OA=3,
∴C(4,7).
∵反比例函数y=图象经过点C,
∴k=4×7=28,
∴反比例函数的解析式为y=$\frac{28}{x}$.
∵OH=OA+AH=3+5=8,
∴点E的横坐标为8,
∴y=$\frac{28}{8}$=$\frac{7}{2}$,
∴点E的纵坐标是$\frac{7}{2}$.
故选C.
点评 本题考查的是反比例函数综合题,涉及到全等三角形的判定与性质、图形旋转的性质等知识,难度适中.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
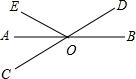 如图,已知直线AB、CD相交于O点,OA平分∠EOC,∠EOC=60°,则∠BOD=30°.
如图,已知直线AB、CD相交于O点,OA平分∠EOC,∠EOC=60°,则∠BOD=30°.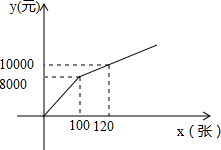 为丰富群众的业余生活,我市准备组织篮球比赛,市体育局策划本次活动,在与单位协商团购票时推出两种方案.设购买门票数为x(张),总费用为y(元).方案一:若单位赞助广告费8000元,则该单位所购门票的价格为每张50元;(总费用=广告赞助费+门票费)
为丰富群众的业余生活,我市准备组织篮球比赛,市体育局策划本次活动,在与单位协商团购票时推出两种方案.设购买门票数为x(张),总费用为y(元).方案一:若单位赞助广告费8000元,则该单位所购门票的价格为每张50元;(总费用=广告赞助费+门票费)