题目内容
18.已知二次函数y=ax2+bx+c的图象经过点(-1,0)、(5,0)、(0、-5).(1)求此二次函数的解析式;
(2)当0≤x≤5时,求此函数的最小值与最大值.
分析 (1)把三个点的坐标代入y=ax2+bx+c得到关于a、b、c的方程组,然后解方程组求出a、b、c的值即可得到抛物线解析式;
(2)根据二次函数的性质求得对称轴和顶点坐标,从而根据开口方向和增减性可得最值.
解答 解:(1)根据题意得$\left\{\begin{array}{l}{a-b+c=0}\\{25a+5b+c=0}\\{c=-5}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=-4}\\{c=-5}\end{array}\right.$,
所以抛物线解析式为y=x2-4x-5;
(2)由(1)中二次函数的解析式可得该二次函数图象的对称轴x=-$\frac{-4}{2}$=2,且函数的开口向上,
当x=2时,y最小=$\frac{4×1×(-5){-(-4)}^{2}}{4}$=-9;
当x=5时,y最大=52-4×5-5=0.
点评 本题主要考查了二次函数的解析式和最值,根据二次函数的性质求最值是解答此题的关键.

练习册系列答案
相关题目
2.抛物线y=ax2+bx+c(a≠0)过(2,8)和(-6,8)两点,则此抛物线的对称轴为( )
| A. | 直线x=0 | B. | 直线x=1 | C. | 直线x=-2 | D. | 直线x=-1 |
8.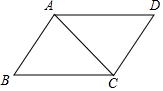 如图,已知AB∥CD,AD∥CB,则△ABC≌△CDA的依据是( )
如图,已知AB∥CD,AD∥CB,则△ABC≌△CDA的依据是( )
 如图,已知AB∥CD,AD∥CB,则△ABC≌△CDA的依据是( )
如图,已知AB∥CD,AD∥CB,则△ABC≌△CDA的依据是( )| A. | SAS | B. | ASA | C. | AAS | D. | SSS |
 如图,在矩形ABCD中,AB=4,BC=2,O为AC的中点,⊙C的半径为1,过点O作⊙C的切线,E为切点,作OF⊥OE,交CD于点F,求tan∠OFC的值.
如图,在矩形ABCD中,AB=4,BC=2,O为AC的中点,⊙C的半径为1,过点O作⊙C的切线,E为切点,作OF⊥OE,交CD于点F,求tan∠OFC的值.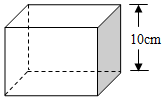 如图,某玩具厂要制作一批体积为1000cm3的长方体包装盒,其高为10cm.按设计需要,底面应做成正方形.求底面边长应是多少?
如图,某玩具厂要制作一批体积为1000cm3的长方体包装盒,其高为10cm.按设计需要,底面应做成正方形.求底面边长应是多少?

 如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=15cm,则△DBE的周长为15cm.
如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=15cm,则△DBE的周长为15cm.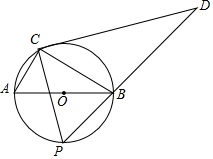 如图,⊙O的直径为4,C为⊙O上一个定点,∠ABC=30°,动点P从A点出发沿半圆弧$\widehat{AB}$向B点运动(点P与点C在直径AB的异侧),当P点到达B点时运动停止,在运动过程中,过点C作CP的垂线CD交PB的延长线于D点.
如图,⊙O的直径为4,C为⊙O上一个定点,∠ABC=30°,动点P从A点出发沿半圆弧$\widehat{AB}$向B点运动(点P与点C在直径AB的异侧),当P点到达B点时运动停止,在运动过程中,过点C作CP的垂线CD交PB的延长线于D点.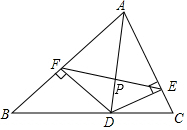 如图,AD是△ABC的角平分线,DF⊥AB于F,DE⊥AC于E,连EF,交AD于点P.
如图,AD是△ABC的角平分线,DF⊥AB于F,DE⊥AC于E,连EF,交AD于点P.