题目内容
13．两条直线l1：y=$\frac{a}{4}$x+b，l2：y=$\frac{1}{2}$x-$\frac{3}{5}$中，当a=2，b=≠-$\frac{3}{5}$时，L1∥L2．分析 利用直线平行的性质求解．
解答 解：∵直线l1：y=$\frac{a}{4}$x+b，l2：y=$\frac{1}{2}$x-$\frac{3}{5}$中，L1∥L2．
∴$\frac{a}{4}=\frac{1}{2}$，b≠-$\frac{3}{5}$，
∴a=2；
故答案为：2，≠-$\frac{3}{5}$．
点评 本题考查了两条直线的平行问题、实数值的求法，是基础题，解题时要认真审题，注意直线平行的性质的灵活运用．
练习册系列答案
名校课堂系列答案
相关题目
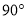,AB=10,BC=6,则AC= _____________。