题目内容
5.如图①、图②、图③,在平面直角坐标系中,抛物线y=a(x-1)2+2-a与抛物线y=(a-2)(x-1)2+a分别与y轴交于点A、B,与对称轴x=1交于点C、D.作点A关于直线x=1的对称点A′,连接AA′,以AB、AA′为边作矩形ABEA′.设△ACD与矩形ABEA′重叠部分图形的面积为S.(1)用含a的代数式表示线段CD的长.
(2)求AB=2AA′时的a值.
(3)当△ACD与矩形ABEA′重叠部分图形为三角形时,求S与a的函数关系式.
(4)作点D关于直线AA′的对称点D′,连接AD、A′D、A′D′、AD′,得到四边形ADA′D′.直接写出四边形ADA′D′与矩形ABEA′同时是正方形时的a值.
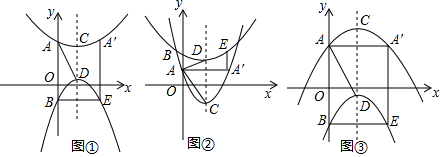
分析 (1)由题意C(1,2-a),D(1,a),可得CD=|2-a-a|=|2-2a|=$\left\{\begin{array}{l}{2-2a}&{(a≤1)}\\{2a-1}&{(a>1)}\end{array}\right.$;
(2)分两种情形①当点A在点B上方时,AB=4-2a,AA′=2.②当点A在点B下方时,AB=2a-4,AA′=2,分别列出方程即可解决问题;
(3)分四种情形①如图1中,当a<0时,重叠部分是△ADH.②如图2中,当0<a<1时,重叠部分是△ACD.③如图3中,当点C在线段BE上时,2a-2=2-a,解得a=$\frac{4}{3}$,当1<a≤$\frac{4}{3}$时,重叠部分是△ADC.④如图4中,当a>2时,重叠部分是△ADH,分别求解即可;
(4)分两种情形点B在点A下方时,点B在点A上方时,分别求解即可;
解答 解:(1)由题意C(1,2-a),D(1,a),
∴CD=|2-a-a|=|2-2a|=$\left\{\begin{array}{l}{2-2a}&{(a≤1)}\\{2a-1}&{(a>1)}\end{array}\right.$.
(2)由题意A(0,2),B(0,2a-2),
①当点A在点B上方时,AB=4-2a,AA′=2,
∴4-2a=4,
∴a=0(不合题意舍弃),
②当点A在点B下方时,AB=2a-4,AA′=2,
∴2a-4=4,
∴a=4,
∴AB=2AA′时的a值为4.
(3)①如图1中,当a<0时,重叠部分是△ADH,S=$\frac{1}{2}$•DH•AH=$\frac{1}{2}$•(2-a)=1-$\frac{1}{2}$a.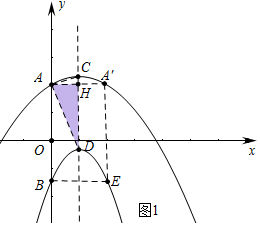
②如图2中,当0<a<1时,重叠部分是△ACD,S=$\frac{1}{2}$•CD•AH=$\frac{1}{2}$(2-2a)=1-a.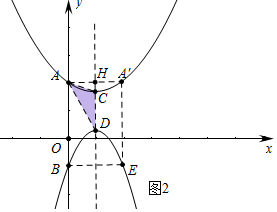
③如图3中,当点C在线段BE上时,2a-2=2-a,解得a=$\frac{4}{3}$,
∴当1<a≤$\frac{4}{3}$时,重叠部分是△ADC,S=$\frac{1}{2}$•CD•AH=$\frac{1}{2}$(2a-2)=a-1.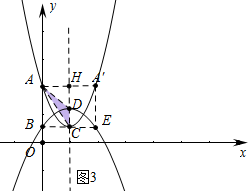
④如图4中,当a>2时,重叠部分是△ADH,S=$\frac{1}{2}$•DH•AH=$\frac{1}{2}$(a-2)=$\frac{1}{2}$a-1.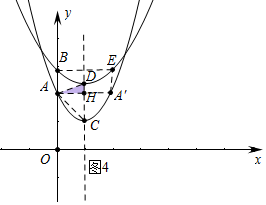
(4)①如图5中,当点B与原点重合时,2a-2=0,即a=1时,满足条件.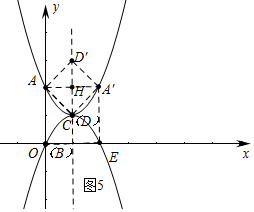
②如图6中,当AB=2,即2a-2=4,解得a=3时,满足条件.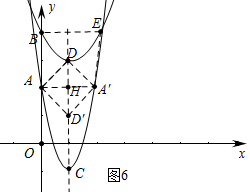
综上所述,四边形ADA′D′与矩形ABEA′同时是正方形时的a值为1或3.
点评 本题考查二次函数综合题、三角形的面积、正方形的性质等知识,解题的关键是学会用分类讨论是思想思考问题,学会构建方程解决问题,属于中考压轴题.

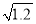 是最简二次根式;
是最简二次根式;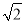 。
。 一慢车和一快车沿相同路线从A地到B地,所行的路程y(千米)与时间x(时)的函数图象如图所示,试根据图象,回答下列问题:
一慢车和一快车沿相同路线从A地到B地,所行的路程y(千米)与时间x(时)的函数图象如图所示,试根据图象,回答下列问题: