题目内容
1.小明要买练习本,他可以到甲商店购买,也可以到乙商店购买.已知两商店的标价都是每本1元,但甲商店的优惠条件是:购买10本以上,从第11本开始按标价的70%卖;乙商店的优惠条件是:从第一本开始就按标价的85%卖;(1)现小明要买20本练习本,他若选择甲商店,需花17元,他若选择乙商店,需花17元.
(2)若小明现有24元钱,他最多可买多少本练习本?
(3)若小明要买x本(x>10)练习本时,到哪个商店购买较省钱?
分析 (1)根据题意,到甲购买10本以上,第11本按标价的70%卖,如果买20本,则付款=10×1+(20-10)×70%×1,那么就可得到(2)中所求的解析式y=0.7x+3,到乙买的解析式为:y=0.85x,然后求出到两个商店的花费,进而比较即可;
(2)可把y=24,分别代入两个解析式,经过比较,可知,到甲买的多;
(3)到甲商店:解析式y=0.7x+3,到乙商店:解析式y=0.85x,当0.7x+3=0.85x时,即x=20时,到两商店买相等,当10<x<20时,选乙商店合算;当x>20时,选甲商店合算.
解答 解:(1)甲店收款为:1×10+1×70%×(20-10)=17(元),
乙店收款为:1×85%×20=17(元);
(2)当x>10时,y=1×10+1×70%(x-10),即y=0.7x+3;
由(1)知,超过17元时,甲商店每本显然低于乙店,故用24元应到甲商店买.当y=24时,即24=0.7x+3,解得x=30.
答:他最多可买30本练习本.
(3)到甲商店:解析式y=0.7x+3,到乙商店:解析式y=0.85x,
当0.7x+3=0.85x时,即x=20时,到两商店买相等,
当10<x<20时,选乙商店合算;
当x>20时,选甲商店合算.
故答案为:17,17.
点评 此题考查了一元一次不等式的应用,一元一次方程的应用,解题时首先认真审题,根据题目给出的条件,找出合适的等量关系,然后解答即可.

(本小题满分8分) 九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设
该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w
(单位:元).
时间x(天) | 1 | 30 | 60 | 90 |
每天销售量p(件) | 198 | 140 | 80 | 20 |
(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.

 的结果是 ( )
的结果是 ( ) B.
B.  C.
C.  D.
D. 
 B. 40
B. 40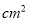 C. 50
C. 50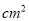 D. 60
D. 60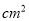
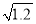 是最简二次根式;
是最简二次根式;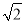 。
。