题目内容
14.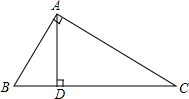 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,BD:CD=1:4.
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,BD:CD=1:4.(1)求tan∠BAD的值;
(2)若AB=$\sqrt{10}$,求AC的长.
分析 (1)设BD=k,DC=4k,先证明△ADB∽△CAD,从而可求得AD=2k,然后利用锐角三角函数的定义求解即可;
(2)在Rt△ABD中,由tan∠BAD=$\frac{1}{2}$,可知sin∠BAD=$\frac{\sqrt{5}}{5}$,cos∠BAD=$\frac{2\sqrt{5}}{5}$,从而可求得BD=$\sqrt{10}×\frac{\sqrt{5}}{5}$=$\sqrt{2}$,AD=2$\sqrt{2}$,然后由△ADB∽△CAD可求得AC=2$\sqrt{10}$.
解答 解:(1)设BD=k,DC=4k.
∵AD⊥BC,
∴∠ADB=∠ADC=90°.
∵∠B+∠BAD=90°,∠BAD+∠DAC=90°,
∴∠B=∠DAC.
∴△ADB∽△CAD.
∴$\frac{AD}{BD}=\frac{DC}{AD}$,即$\frac{AD}{k}=\frac{4k}{AD}$.
解得:AD=2k.
∴tan∠BAD=$\frac{BD}{AD}=\frac{k}{2k}=\frac{1}{2}$.
(2)∵tan∠BAD=$\frac{1}{2}$,
∴sin∠BAD=$\frac{\sqrt{5}}{5}$,cos∠BAD=$\frac{2\sqrt{5}}{5}$.
又∵AB=$\sqrt{10}$,
∴BD=$\sqrt{10}×\frac{\sqrt{5}}{5}$=$\sqrt{2}$,AD=2$\sqrt{2}$.
∵△ADB∽△CAD,
∴$\frac{AB}{BD}=\frac{AC}{AD}$,即$\frac{\sqrt{10}}{\sqrt{2}}=\frac{AC}{2\sqrt{2}}$.
∴AC=2$\sqrt{10}$.
点评 本题主要考查的是相似三角形的性质和判定、解直角三角形,掌握相似三角形的性质和判定是解题的关键.

| A. | +1或+7 | B. | -1或-7 | C. | +1或-7 | D. | -1或+7 |
| A. | (0,1) | B. | (1,2) | C. | (2,1) | D. | (2,0) |
 如图,已知线段AB=6,在平面上有一动点P恒满足PA-PB=4,过点A作∠APB的角平分线的垂线,垂足为M,则△AMB的面积的最大值是6.
如图,已知线段AB=6,在平面上有一动点P恒满足PA-PB=4,过点A作∠APB的角平分线的垂线,垂足为M,则△AMB的面积的最大值是6.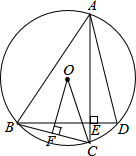 如图.点A、B、C、D在⊙O上,AC⊥BD于点E,过点O作OF⊥BC于F,
如图.点A、B、C、D在⊙O上,AC⊥BD于点E,过点O作OF⊥BC于F, 如图,已知E是平行四边形ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F.
如图,已知E是平行四边形ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F. 如图:抛物线y1=$\frac{1}{2}$x2+(m-5)x+2m与直线y2=2x-4交于x轴上A点和另一点B.
如图:抛物线y1=$\frac{1}{2}$x2+(m-5)x+2m与直线y2=2x-4交于x轴上A点和另一点B.