题目内容
19. 如图,已知E是平行四边形ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F.
如图,已知E是平行四边形ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F.(1)求证:△ABE≌△FCE;
(2)连接AC、BF,若AE=$\frac{1}{2}$BC,求证:四边形ABFC为矩形;
(3)在(2)条件下,当△ABC再满足一个什么条件时,四边形ABFC为正方形.
分析 (1)由平行四边形的性质得出AB∥CD,AB=CD,得出∠BAE=∠EFC,由AAS证明△ABE≌△FCE即可;
(2)由全等三角形的对边相等得出AB=FC,由BE=CE,得出四边形ABFC为平行四边形,证出BC=AF,即可得出四边形ABFC是矩形;
(3)由等腰三角形的三线合一性质得出AE⊥BC,得出四边形ABFC是菱形,即可得出结论四边形ABFC为正方形.
解答 (1)证明:在平行四边形ABCD中,AB∥CD,AB=CD,
∴∠BAE=∠EFC,
∵E为BC的中点,
∴BE=EC,
在△ABE和△FCE中,
$\left\{\begin{array}{l}{∠BAE=∠EFC}&{\;}\\{∠AEB=∠FEC}&{\;}\\{BE=CE}&{\;}\end{array}\right.$,
∴△ABE≌△FCE(AAS),
(2)证明:∵△ABE≌△FCE,
∴AB=FC,
∵BE=CE,
∴四边形ABFC为平行四边形,
∵AE=EF=$\frac{1}{2}$AF,AE=$\frac{1}{2}$BC,
∴BC=AF,
∴四边形ABFC是矩形;
(3)解:当△ABC为等腰三角形时,即AB=AC时,四边形ABFC为正方形;理由如下:
∵AB=AC,E为BC的中点,
∴AE⊥BC,
∵四边形ABFC为平行四边形,
∴四边形ABFC是菱形,
又∵四边形ABFC是矩形,
∴四边形ABFC为正方形.
点评 本题考查了平行四边形的判定与性质、全等三角形的判定与性质、矩形的判定、正方形的判定方法、等腰三角形的性质;本题综合性强,难度适中,证明三角形全等和平行四边形是解决问题的关键.

练习册系列答案
相关题目
10.$\sqrt{{x^2}-4x+4}$=x-2,则( )
| A. | x>-2 | B. | x≥2 | C. | x<-2 | D. | x≥-2 |
4.若|a-1|+|b-2|=0,那么2ab=( )
| A. | -4 | B. | +4 | C. | -8 | D. | +8 |
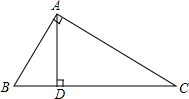 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,BD:CD=1:4.
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,BD:CD=1:4.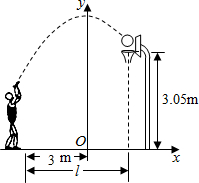 如图,小姚身高$\frac{9}{4}$m在某次投篮中,球的运动路线是抛物线y=-$\frac{1}{5}$x2+$\frac{7}{2}$的一部分,若命中篮圈中心,则他与篮底的距离是( )
如图,小姚身高$\frac{9}{4}$m在某次投篮中,球的运动路线是抛物线y=-$\frac{1}{5}$x2+$\frac{7}{2}$的一部分,若命中篮圈中心,则他与篮底的距离是( )