题目内容
5. 如图,O是正方形ABCD的中心,M是ABCD内一点,∠DMC=90°,将△DMC绕O点旋转180°后得到△NAB,若MD=3,CM=4,则MN的长为$\sqrt{2}$.
如图,O是正方形ABCD的中心,M是ABCD内一点,∠DMC=90°,将△DMC绕O点旋转180°后得到△NAB,若MD=3,CM=4,则MN的长为$\sqrt{2}$.
分析 延长DM交AN于E,延长BN交CM于F,根据旋转的性质得到∠ANB=∠CMD=90°,AN∥CM,根据余角的性质得到∠EAD=∠CDM,根据全等三角形的性质得到AE=DM=3,DE=CM=4,推出四边形ENFM是正方形,根据勾股定理即可得到结论.
解答 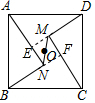 解:延长DM交AN于E,延长BN交CM于F,
解:延长DM交AN于E,延长BN交CM于F,
∵∠DMC=90°,将△DMC绕O点旋转180°后得到△NAB,
∴∠ANB=∠CMD=90°,AN∥CM,
∴∠MEN=∠DMC=∠ANB=∠BFC=90°,
∴∠DAE+∠ADE=∠ADE+∠CDM=90°,
∴∠EAD=∠CDM,
在△ADE与△CDM中,$\left\{\begin{array}{l}{∠AED=∠DMC=90°}\\{∠EAD=∠MDC}\\{AD=CD}\end{array}\right.$,
∴△ADE≌△CDM,
∴AE=DM=3,DE=CM=4,
∴ME=1,
∴EN=1,
同理MF=FN=1,
∴四边形ENFM是正方形,
∴MN=$\sqrt{2}$,
故答案为:$\sqrt{2}$.
点评 本题考查了旋转的性质,正方形的性质,全等三角形的判定和性质,则的作出辅助线是解题的关键.

练习册系列答案
相关题目
 如图,在平面直角坐标系中,⊙P的半径为4,圆心P坐标是(4,a)(a>4),函数y=x的图象被⊙P截得的弦AB的长为4$\sqrt{3}$,则a的值是4+2$\sqrt{2}$.
如图,在平面直角坐标系中,⊙P的半径为4,圆心P坐标是(4,a)(a>4),函数y=x的图象被⊙P截得的弦AB的长为4$\sqrt{3}$,则a的值是4+2$\sqrt{2}$.
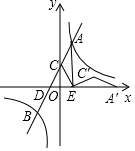 已知一次函数y1=k1x+b与反比例函数y2=$\frac{{k}_{2}}{x}$相交于点A、B,与y轴交于点C,与x轴交于点D,过点A作AE⊥x轴于点E,点O为DE中点,连接CE,已知S△ADE=4,tan∠DCO=$\frac{1}{2}$.
已知一次函数y1=k1x+b与反比例函数y2=$\frac{{k}_{2}}{x}$相交于点A、B,与y轴交于点C,与x轴交于点D,过点A作AE⊥x轴于点E,点O为DE中点,连接CE,已知S△ADE=4,tan∠DCO=$\frac{1}{2}$. 如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )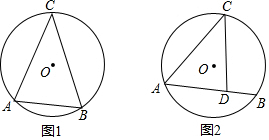

 某校王老师组织九(1)班同学开展数学活动,某天带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A的仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高AB.(结果用根号表示)
某校王老师组织九(1)班同学开展数学活动,某天带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A的仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高AB.(结果用根号表示)