��Ŀ����
7����֪���κ���ͼ��Ķ�������ΪC��-1��0����ֱ��y=-x+m��ö��κ���y=ax2+bx+c��ͼ����A��B���㣬����A�������Ϊ��-3��4����B����y���ϣ�PΪֱ��AB�ϵ�һ�����㣨��P��A��B���غϣ�����P��x��Ĵ�����������κ�����ͼ���ڵ�E��DΪֱ��AB��������κ���ͼ��ĶԳ���Ľ��㣮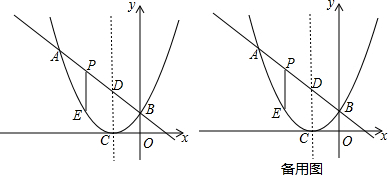
��1����m��ֵ��������κ����Ľ���ʽ��
��2�����߶�AB���Ƿ����һ��P��ʹ���ı���DCEP��ƽ���ı��Σ������ڣ��������ʱP������ꣻ�������ڣ���˵�����ɣ�
��3�����������Ƿ���ڵ�E��ʹS��EAB=3�������ڣ���ֱ��д����ʱE������ꣻ�������ڣ���˵�����ɣ�
���� ��1�����ݶ������꣨-1��0���������ߵĽ���ʽΪ��y=a��x+1��2���ѵ�A��-3��4���ֱ������κ�����һ�κ����Ľ���ʽ�пɵý��ۣ�
��2������AB�Ľ���ʽ�����ݽ���ʽ��ʾ��P��E��������꣺��P��x��-x+1����E��x��x2+2x+1������ƽ���ı��ε����ʣ�CD=PE��ʽ�����x��ֵ�������P�����ꣻ
��3���������������ͼ2����E��AB���·�ʱ���������������=Ǧֱ�ߡ�ˮƽ������ʱ��ˮƽ����3��Ǧֱ����EF�����ݽ���ʽ��ʾ�������=2���������ý��ۣ�
��ͼ3����E��AB���Ϸ�ʱ��
��ͼ2��֪����ABƽ��������ƽ��2����λ��ֱ��EF�Ľ���ʽΪ��y=-x+3����ֱ���������ߵĽ��㼴�ǵ�E���з�����������ɣ�
��� �⣺��1����A��-3��4������y=-x+m�ã�3+m=4��
m=1��
�������ߵĽ���ʽΪ��y=a��x+1��2��
��A��-3��4������y=a��x+1��2�еã�a��-3+1��2=4��
a=1��
��������κ����Ľ���ʽΪ��y=��x+1��2=x2+2x+1��
��2����ͼ1����x=0ʱ��y=1��
��B��0��1����
��ֱ��AB�Ľ���ʽΪ��y=kx+b��
��A��-3��4����B��0��1������ã�$\left\{\begin{array}{l}{-3k+b=4}\\{b=1}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-1}\\{b=1}\end{array}\right.$��
��ֱ��AB�Ľ���ʽΪ��y=-x+1��
��x=-1ʱ��y=1+1=2��
��D��-1��2����
��CD=2��
��P��x��-x+1����E��x��x2+2x+1����
���ı���DCEP��ƽ���ı��Σ�
��CD=PE��CD��PE��
��PE=��-x+1��-��x2+2x+1��=-x2-3x=2��
x2+3x+2=0��
��x+1����x+2��=0��
x1=-1���ᣩ��x2=-2��
��x=-2ʱ��y=2+1=3��
��P��-2��3����
��3�����ڣ�
��E��EF��CD����AB��F
��F��x��-x+1����E��x��x2+2x+1����
��S��ABE=$\frac{1}{2}$��3EF=3
��EF=2
��ͼ2����E��AB���·�ʱ��
EF=��-x+1��-��x2+2x+1��=-x2-3x=2��
x1=-1��x2=-2��
��x=-1ʱ��y=0��
��x=-2ʱ��y=1��
��ʱ��E��-1��0������-2��1����
��ͼ3����E��AB���Ϸ�ʱ��
��ͼ2��֪����ABƽ��������ƽ��2����λ��ֱ��EF�Ľ���ʽΪ��y=-x+3��
��$\left\{\begin{array}{l}{y=-x+3}\\{y={x}^{2}+2x+1}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{{x}_{1}=\frac{-3+\sqrt{17}}{2}}\\{{y}_{1}=\frac{9-\sqrt{17}}{2}}\end{array}\right.$ $\left\{\begin{array}{l}{{x}_{2}=\frac{-3-\sqrt{17}}{2}}\\{{y}_{2}=\frac{9+\sqrt{17}}{2}}\end{array}\right.$��
��E��$\frac{-3+\sqrt{17}}{2}$��$\frac{9-\sqrt{17}}{2}$����$\frac{-3-\sqrt{17}}{2}$��$\frac{9+\sqrt{17}}{2}$����
������������E����������-1��0����-2��1����$\frac{-3+\sqrt{17}}{2}$��$\frac{9-\sqrt{17}}{2}$����$\frac{-3-\sqrt{17}}{2}$��$\frac{9+\sqrt{17}}{2}$����
���� ���⿼���˴���ϵ��������κ����Ľ���ʽ�������ô���ϵ��������κ�����ϵʽʱ��Ҫ������Ŀ������������ѡ��ǡ���ķ��������ϵʽ���Ӷ�������ֵ��⣮һ��أ�����֪������������ʱ����ѡ��һ��ʽ���ô���ϵ��������Ԫһ�η���������⣻����֪�����ߵĶ����Գ���ʱ�����������ʽΪ����ʽ����������趥��ʽ�������ʽ��������֪�����������ֵ��ȷ����������һ��������ʱ��������ȷ��ƽ���߽���ʽ�ķ������������������Ľ�����������⣮

| A�� | �ڡ�A�� | B�� | �ڡ�A�� | C�� | �ڡ�A�� | D�� | ����ȷ�� |
| A�� | ��-2��1�� | B�� | ��-2��-$\frac{3}{2}$�� | C�� | ��-$\frac{3}{2}$��-9�� | D�� | ��-2��-1�� |

 ��ͼ����ABC�У���A������Ϊ��0��1������C������Ϊ��4��3������B������Ϊ��3��1�������Ҫʹ��ABD���ABCȫ�ȣ�
��ͼ����ABC�У���A������Ϊ��0��1������C������Ϊ��4��3������B������Ϊ��3��1�������Ҫʹ��ABD���ABCȫ�ȣ�