题目内容
19.在坐标平面上有一个轴对称图形,其中A(3,-$\frac{5}{2}$)和B(3,-$\frac{11}{2}$)是图形上的一对对称点,若此图形上另有一点C(-2,-9),则C点对称点的坐标是( )| A. | (-2,1) | B. | (-2,-$\frac{3}{2}$) | C. | (-$\frac{3}{2}$,-9) | D. | (-2,-1) |
分析 先利用点A和点B的坐标特征可判断图形的对称轴为直线y=-4,然后写出点C关于直线y=-4的对称点即可.
解答 解:∵A(3,-$\frac{5}{2}$)和B(3,-$\frac{11}{2}$)是图形上的一对对称点,
∴点A与点B关于直线y=-4对称,
∴点C(-2,-9)关于直线y=-4的对称点的坐标为(-2,1).
故选A.
点评 本题考查了坐标与图形变化-对称:记住关于坐标轴对称的点的坐标特征,理解关于直线对称:①关于直线x=m对称,P(a,b)⇒P(2m-a,b),②关于直线y=n对称,P(a,b)⇒P(a,2n-b).

练习册系列答案
相关题目
9.下列语句中,正确的事( )
| A. | 一个命题一定有逆命题 | B. | 一个定理一定有逆定理 | ||
| C. | 命题真,它的逆命题也一定真 | D. | 命题假,它的逆命题也一定假 |
10.下列各式中,与3-19+5的值相等的是( )
| A. | 3+(-19)-(-5) | B. | -3+(-19)+(-5) | C. | -3+(-19)+5 | D. | 3-(+19)-(+5) |
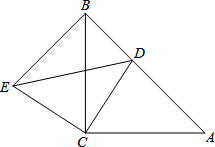 如图,△ABC与△CDE均是等腰直角三角形,∠ACB=∠ECD=90°,点D在AB上,连接BE.
如图,△ABC与△CDE均是等腰直角三角形,∠ACB=∠ECD=90°,点D在AB上,连接BE.