题目内容
16. 一个装有进水管和出水管的容器,根据实际需要,从某时刻开始的2分钟内只进水不出水,在随后的4分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的部分关系如图所示.
一个装有进水管和出水管的容器,根据实际需要,从某时刻开始的2分钟内只进水不出水,在随后的4分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的部分关系如图所示.(1)当2≤x≤6时,求y与x的表达式;
(2)请将图象补充完整;
(3)从进水管开始进水起,求该容器内的水量不少于7.5升所持续时间.
分析 (1)利用待定系数法即可解决.
(2)求出关闭进水管直到容器内的水放完需要的时间,画出图象即可解决问题.
(3)根据0≤x≤2时,y与x的函数表达式为y=5 x,以及6≤x≤10时,y与x的函数表达式为y=-$\frac{15}{4}$x+$\frac{75}{2}$,分别求出y=7.5时的时间,求出两个时间的差即可解决问题.
解答 解:(1)设y与x的函数表达式为y=kx+b
将点( 2,10 ),( 6,15)代入y=kx+b得:
$\left\{\begin{array}{l}2k+b=10\\ 6k+b=15\end{array}$ 解得 $\left\{\begin{array}{l}k=\frac{5}{4}\\ b=\frac{5}{2}\end{array}$
∴当2≤x≤6时,y与x的函数表达式为y=$\frac{5}{4}$ x+$\frac{15}{2}$.
(2)由题意可求出进水管每分钟的进水量为5升,出水管每分钟的出水量为3.75升,
故关闭进水管直到容器内的水放完需要4分钟.所以补充的图象为连接点( 6,15 )
和点(10,0 )所得的线段.图象如图所示,
(3)由题意可求:当0≤x≤2时,y与x的函数表达式为y=5 x
当6≤x≤10时,y与x的函数表达式为y=-$\frac{15}{4}$x+$\frac{75}{2}$
把y=7.5代入y=5 x,得x1=1.5
把y=7.5代入y=-$\frac{15}{4}$x+$\frac{75}{2}$,得x2=8,
∴该容器内的水量不少于7.5升的持续时间为x2-x1=8-1.5=6.5(分钟)
答:该容器内的水量不少于7.5升的持续时间为6.5分钟.
点评 本题考查一次函数的应用、待定系数法等知识,解题的关键是学会构建一次函数,利用一次函数解决实际问题,属于中考常考题型.

 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案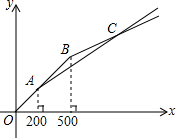 “五一”期间,甲、乙两家商店以同样价格销售相同的商品,两家优惠方案分别为:甲店一次性购物中超过200元后的价格部分打七折;乙店一次性购物中超过500元后的价格部分打五折,设商品原价为x元(x≥0),购物应付金额为y元.
“五一”期间,甲、乙两家商店以同样价格销售相同的商品,两家优惠方案分别为:甲店一次性购物中超过200元后的价格部分打七折;乙店一次性购物中超过500元后的价格部分打五折,设商品原价为x元(x≥0),购物应付金额为y元.