题目内容
6.解方程(组)或不等式(1)3x-5≤5x-(3-x)
(2)$\frac{x-3}{2}$-$\frac{4x+1}{5}$=1
(3)$\left\{\begin{array}{l}{x+3y=-1}\\{3x-2y=8}\end{array}\right.$
(4)$\left\{\begin{array}{l}{y-3x=-7}\\{5x+2y=8}\end{array}\right.$.
分析 (1)先去括号,再移项、合并得到-3x≤2,然后把x的系数化为1即可;
(2)先去括号、移项合并得到-3x=27,然后把x的系数化为1即可;
(3)利用加减消元法解方程组;
(4)利用加减消元法解方程组.
解答 解:(1)去括号得3x-5≤5x-3+x,
移项得3x-5x-x≤-3+5,
合并得-3x≤2,
系数化为1得x≥-$\frac{2}{3}$;
(2)去分母得5(x-3)-2(4x+1)=10,
去括号得5x-15-8x-2=10,
合并得-3x=27,
系数化为1得x=-9;
(3)$\left\{\begin{array}{l}{x+3y=-1①}\\{3x-2y=8②}\end{array}\right.$,
①×3-②得9y+2y=-3-8,
解得y=-1,
把y=-1代入①得x-3=-1,
解得x=2,
所以方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$;
(4)$\left\{\begin{array}{l}{y-3x=-7①}\\{5x+2y=8②}\end{array}\right.$,
①×2-②得-6x-5x=-14-8,
解得x=2,
把x=2代入①得y-6=-7,
解得y=-1,
所以方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$.
点评 本题考查了解一元一次不等式:根据不等式的性质解一元一次不等式,基本操作方法与解一元一次方程基本相同,都有如下步骤:①去分母;②去括号;③移项;④合并同类项;⑤化系数为1.也考查了解二元一次方程组.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
6.某宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与其价格x(元)(180≤x≤300)满足一次函数关系,部分对应值如表:
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每日空置的客房需支出各种费用60元,当房价为多少元时,宾馆当日利润最大?求出最大值.(宾馆当日利润=当日房费收入-当日支出)
| x(元) | 180 | 260 | 280 | 300 |
| y(间) | 100 | 60 | 50 | 40 |
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每日空置的客房需支出各种费用60元,当房价为多少元时,宾馆当日利润最大?求出最大值.(宾馆当日利润=当日房费收入-当日支出)
14.若(m+2)x${\;}^{{m}^{2}-3}$-2m=1,是关于x的一元一次方程,则m=( )
| A. | ±2 | B. | 2 | C. | -2 | D. | 1 |
18.计算-3+|-5|的结果是( )
| A. | -2 | B. | 2 | C. | -8 | D. | 8 |
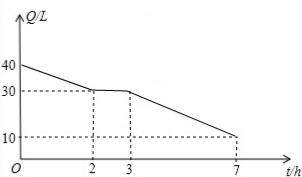
 一个装有进水管和出水管的容器,根据实际需要,从某时刻开始的2分钟内只进水不出水,在随后的4分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的部分关系如图所示.
一个装有进水管和出水管的容器,根据实际需要,从某时刻开始的2分钟内只进水不出水,在随后的4分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的部分关系如图所示.