题目内容
8.化简下列各式:(1)(a+b)(a-2b)-(a-b)2
(2)$(\frac{{{x^2}-9}}{{{x^2}-6x+9}}-\frac{1}{3-x})÷(\frac{7}{x-3}-x-3)$.
分析 (1)根据多项式乘以多项式、完全平方公式可以对原式进行化简;
(2)先化简括号内的式子,然后根据分式的除法进行计算即可解答本题.
解答 解:(1)(a+b)(a-2b)-(a-b)2
=a2-ab-2b2-a2+2ab-b2
=ab-3b2;
(2)$(\frac{{{x^2}-9}}{{{x^2}-6x+9}}-\frac{1}{3-x})÷(\frac{7}{x-3}-x-3)$
=[$\frac{(x+3)(x-3)}{(x-3)^{2}}$-$\frac{1}{3-x}$]÷$\frac{7-(x+3)(x-3)}{x-3}$
=$\frac{{x}^{2}-9+x-3}{(x-3)^{2}}$×$\frac{x-3}{7-{x}^{2}+9}$
=$\frac{{x}^{2}+x-12}{x-3}×\frac{1}{16-{x}^{2}}$
=$\frac{(x+4)(x-3)}{x-3}×\frac{1}{(4+x)(4-x)}$
=$\frac{1}{4-x}$.
点评 本题考查分式的混合运算、多项式乘以多项式、完全平方公式,解题的关键是明确它们各自的计算方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.计算-3+|-5|的结果是( )
| A. | -2 | B. | 2 | C. | -8 | D. | 8 |
17.下列说法中正确的是( )
| A. | $\sqrt{4}$是一个无理数 | B. | $\sqrt{81}$的平方根是±3 | ||
| C. | 8的立方根是±2 | D. | 一个数的算术平方根一定是正数 |
 一个装有进水管和出水管的容器,根据实际需要,从某时刻开始的2分钟内只进水不出水,在随后的4分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的部分关系如图所示.
一个装有进水管和出水管的容器,根据实际需要,从某时刻开始的2分钟内只进水不出水,在随后的4分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的部分关系如图所示.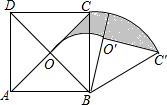 如图,正方形ABCD中,对角线AC、BD相交于点O,△OBC绕点B顺时针旋转60°得到△0′BC′,若AB=2,则图中阴影部分的面积是 $\frac{π}{3}$.
如图,正方形ABCD中,对角线AC、BD相交于点O,△OBC绕点B顺时针旋转60°得到△0′BC′,若AB=2,则图中阴影部分的面积是 $\frac{π}{3}$.