题目内容
12.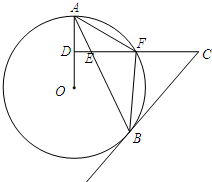 如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.(1)求证:BC是⊙O的切线;
(2)如果CD=15,BE=10,sin∠DAE=$\frac{5}{13}$,求⊙O的半径.
分析 (1)连接OB,由圆的半径相等和已知条件证明∠OBC=90°,即可证明BC是⊙O的切线;
(2)过点C作CG⊥BE于G,根据等腰三角形的性质得到EG=$\frac{1}{2}$BE=5,由两角相等的三角形相似,△ADE∽△CGE,利用相似三角形对应角相等得到sin∠ECG=sinDAE=$\frac{5}{13}$,在Rt△ECG中,利用勾股定理求出CG的长,根据三角形相似得到比例式,代入数据即可得到结果.
解答  (1)证明:连接OB,如图1所示:
(1)证明:连接OB,如图1所示:
∵OB=OA,CE=CB,
∴∠A=∠OBA,∠CEB=∠ABC,
又∵CD⊥OA,
∴∠A+∠AED=∠A+∠CEB=90°,
∴∠OBA+∠ABC=90°,
∴OB⊥BC,
∴BC是⊙O的切线;
(2)解:如图2,过点C作CG⊥BE于G,
∵CE=CB,
∴EG=$\frac{1}{2}$BE=5,
∵∠ADE=∠CGE=90°,∠AED=∠GEC,
∴∠GCE=∠A,
∴△ADE∽△CGE,
∴sin∠ECG=sinA=$\frac{EG}{CE}$=$\frac{5}{13}$,
∴CE=13,
在Rt△ECG中,
∵CG=$\sqrt{C{E}^{2}-E{G}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12,
∵CD=15,CE=13,
∴DE=2,
∵△ADE∽△CGE,
∴$\frac{AD}{CG}=\frac{DE}{GE}$,
∴AD=$\frac{DE}{GE}$•CG=$\frac{24}{5}$,
∴⊙O的半径OA=2AD=$\frac{48}{5}$.
点评 此题考查了切线的判定,勾股定理,三角函数,等腰三角形的性质以及相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
3.在学校开展的“争做最优秀中学生”的一次演讲比赛中,编号分别为1,2,3,4,5的五位同学最后成绩如下表所示:
那么这五位同学演讲成绩的众数与中位数依次是( )
| 参赛者编号 | 1 | 2 | 3 | 4 | 5 |
| 成绩(分) | 96 | 88 | 86 | 93 | 86 |
| A. | 96,88 | B. | 92,88 | C. | 88,86 | D. | 86,88 |
20.不等式组$\left\{\begin{array}{l}{-2x+3≤5}\\{3(x-1)<x+7}\end{array}\right.$的解集为( )
| A. | x≤-1 | B. | -1≤x<5 | C. | 1≤x<5 | D. | -1≤x<2 |
4.某校在中国学生核心素养知识竞赛中,通过激烈角逐,甲、乙、丙、丁四名同学胜出,他们2的成绩如表:
如果要选出一个成绩较好且状态稳定的同学去参加市级比赛,应选( )
| 甲 | 乙 | 丙 | 丁 | |
| 平均分 | 8.5 | 8.2 | 8.5 | 8.2 |
| 方差 | 1.8 | 1.2 | 1.2 | 1.1 |
| 最高分 | 9.8 | 9.8 | 9.8 | 9.7 |
| A. | 丁 | B. | 丙 | C. | 乙 | D. | 甲 |
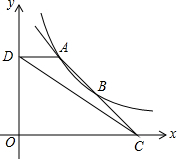 如图,直线y=mx+n与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A、B两点,交x轴于点C($\frac{9}{2}$,0),过点A作AD⊥y轴于点D(0,$\frac{8}{3}$),连接CD,S△ADC=2.
如图,直线y=mx+n与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A、B两点,交x轴于点C($\frac{9}{2}$,0),过点A作AD⊥y轴于点D(0,$\frac{8}{3}$),连接CD,S△ADC=2.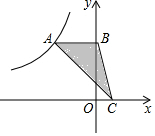 如图,在平面直角坐标系中,点A是函数y=$\frac{k}{x}$(x<0)图象上的点,过点A作y轴的垂线交y轴于点B,点C在x轴上,若△ABC的面积为1,则k的值为-2.
如图,在平面直角坐标系中,点A是函数y=$\frac{k}{x}$(x<0)图象上的点,过点A作y轴的垂线交y轴于点B,点C在x轴上,若△ABC的面积为1,则k的值为-2. 如图,将平行四边形ABCD沿对角线AC折叠,使点B落在点B′处.若∠1=∠2=44°,则∠D=114度.
如图,将平行四边形ABCD沿对角线AC折叠,使点B落在点B′处.若∠1=∠2=44°,则∠D=114度.