题目内容
1. 如图,将平行四边形ABCD沿对角线AC折叠,使点B落在点B′处.若∠1=∠2=44°,则∠D=114度.
如图,将平行四边形ABCD沿对角线AC折叠,使点B落在点B′处.若∠1=∠2=44°,则∠D=114度.
分析 由平行四边形的性质和折叠的性质得出∠ACD=∠BAC=∠B′AC,由三角形的外角性质求出∠BAC=∠ACD=∠B′AC=$\frac{1}{2}$∠1=22°,再由三角形内角和定理求出∠B,再根据平行四边形的性质求出∠D即可.
解答 解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ACD=∠BAC,
由折叠的性质得:∠BAC=∠B′AC,
∴∠BAC=∠ACD=∠B′AC=$\frac{1}{2}$∠1=22°,
∴∠B=180°-∠2-∠BAC=180°-44°-22°=114°,
∴∠D=∠B=114°.
故答案为:114.
点评 本题考查了平行四边形的性质、折叠的性质、三角形的外角性质以及三角形内角和定理;熟练掌握平行四边形的性质,求出∠BAC的度数是解决问题的关键.

练习册系列答案
相关题目
9.生活中处处有数学,下列原理运用错误的是( )
| A. | 建筑工人砌墙时拉的参照线是运用“两点之间线段最短”的原理 | |
| B. | 修理损坏的椅子腿时斜钉的木条是运用“三角形稳定性”的原理 | |
| C. | 测量跳远的成绩是运用“垂线段最短”的原理 | |
| D. | 将车轮设计为圆形是运用了“圆的旋转对称性”原理 |
11.以一个面积为1的三角形的三条中位线为三边的三角形的面积为( )
| A. | 4 | B. | 2 | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
 如图,点D是等边△ABC内一点,DA=8,BD=10,CD=6,则∠ADC的度数是150°.
如图,点D是等边△ABC内一点,DA=8,BD=10,CD=6,则∠ADC的度数是150°.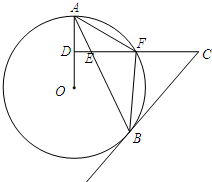 如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.