题目内容
2.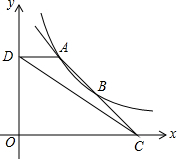 如图,直线y=mx+n与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A、B两点,交x轴于点C($\frac{9}{2}$,0),过点A作AD⊥y轴于点D(0,$\frac{8}{3}$),连接CD,S△ADC=2.
如图,直线y=mx+n与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A、B两点,交x轴于点C($\frac{9}{2}$,0),过点A作AD⊥y轴于点D(0,$\frac{8}{3}$),连接CD,S△ADC=2.(1)求反比例函数y=$\frac{k}{x}$与直线y=mx+n的表达式;
(2)求△DAB的面积;
(3)直接写出关于x的不等式mx+n<$\frac{k}{x}$的解集.
分析 (1)连接OA,根据三角形的面积得到k=±4.于是得到y=$\frac{4}{x}$;然后根据待定系数法确定函数关系式;
(2)解方程组得到A($\frac{3}{2}$,$\frac{8}{3}$),B(3,$\frac{4}{3}$),根据三角形的面积公式即可得到结论;
(3)根据图象,观察即可求得答案.
解答  解:(1)连接OA,
解:(1)连接OA,
∵S△DAO=$\frac{1}{2}$•AD•DO=S△DAC=2,S△DAO=$\frac{|k|}{2}$,
∴k=±4.
∵k>0,∴k=4,
∴y=$\frac{4}{x}$;
∵D(0,$\frac{8}{3}$),
∴yD=$\frac{8}{3}$,
∵yA=yD=$\frac{8}{3}$,$\frac{8}{3}$=$\frac{4}{{x}_{A}}$,解得xA=$\frac{3}{2}$,即A($\frac{3}{2}$,$\frac{8}{3}$),
∵直线y=mx+n过点A($\frac{3}{2}$,$\frac{8}{3}$)和C($\frac{9}{2}$,0),
∴$\left\{\begin{array}{l}\frac{3}{2}m+n=\frac{8}{3}\\ \frac{9}{2}m+n=0\end{array}$ 解得$\left\{\begin{array}{l}m=-\frac{8}{9}\\ n=4\end{array}$,
∴y=-$\frac{8}{9}$x+4;
(2)联立:$\left\{\begin{array}{l}y=\frac{4}{x}\\ y=-\frac{8}{9}x+4\end{array}$ 解得:$\left\{\begin{array}{l}x=\frac{3}{2}\\ y=\frac{8}{3}\end{array}$ 或 $\left\{\begin{array}{l}x=3\\ y=\frac{4}{3}\end{array}$.
∴A($\frac{3}{2}$,$\frac{8}{3}$),B(3,$\frac{4}{3}$),
∵A($\frac{3}{2}$,$\frac{8}{3}$),∴AD=$\frac{3}{2}$,
S△DAB=$\frac{1}{2}$•AD•yB=$\frac{1}{2}$•$\frac{3}{2}$×$\frac{4}{3}$=1;
(3)由图象知,不等式mx+n<$\frac{k}{x}$的解集为0<x<$\frac{3}{2}$或x>3.8.
点评 此题考查了反比例函数与一次函数的交点问题.注意待定系数法的应用是解题的关键.

| A. | 7×105 | B. | 7×106 | C. | 70×106 | D. | 7×107 |
 如图,直线AB与CD相交于点O,若∠1+∠2=80°,则∠3等于( )
如图,直线AB与CD相交于点O,若∠1+∠2=80°,则∠3等于( )| A. | 100° | B. | 120° | C. | 140° | D. | 160° |
| A. | 3.28×102 | B. | 32.8×105 | C. | 3.28×106 | D. | 3.28×107 |
 如图,Rt△OAB的边OA在x轴上,点B在第一象限,点D是斜边OB的中点,反比例函数y=$\frac{k}{x}$经过点D,若S△AOD=6,则k=6.
如图,Rt△OAB的边OA在x轴上,点B在第一象限,点D是斜边OB的中点,反比例函数y=$\frac{k}{x}$经过点D,若S△AOD=6,则k=6. 如图,⊙O的内接正三角形ABC的边心距OD为2cm,则⊙O的半径为4cm.
如图,⊙O的内接正三角形ABC的边心距OD为2cm,则⊙O的半径为4cm. 如图,点D是等边△ABC内一点,DA=8,BD=10,CD=6,则∠ADC的度数是150°.
如图,点D是等边△ABC内一点,DA=8,BD=10,CD=6,则∠ADC的度数是150°.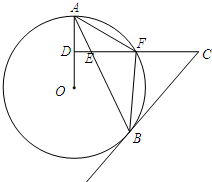 如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.