题目内容
 如图,直线AB与CD相交于点O,射线OF,OD分别是∠AOE,∠BOE的角平分线.
如图,直线AB与CD相交于点O,射线OF,OD分别是∠AOE,∠BOE的角平分线.(1)请写出∠EOF的所有余角:
(2)请写出∠DOE的所有补角:
(3)若∠AOC=
| 1 |
| 6 |
(4)试问射线OD与OF之间有什么特殊的位置关系?为什么?
考点:余角和补角
专题:
分析:(1)根据互余的定义确定∠EOF的余角;
(2)根据互补的定义确定∠DOE的补角;
(3)先根据角平分线的定义得出∠FOD的度数,再由∠AOC=
∠FOB,设∠AOC=x°,则∠FOB=6x°然后根据∠FOD=90°,即可列方程求得x的值,进而求解;
(4)运用平角的定义和角平分线的定义,证明∠DOF是90°,得直线OD、OF的位置关系.
(2)根据互补的定义确定∠DOE的补角;
(3)先根据角平分线的定义得出∠FOD的度数,再由∠AOC=
| 1 |
| 6 |
(4)运用平角的定义和角平分线的定义,证明∠DOF是90°,得直线OD、OF的位置关系.
解答:解:(1)∠EOF的所有余角:∠EOD、∠BOD、∠AOC;
(2)∠DOE的所有补角:∠COE、∠AOD;
(3)设∠AOC=x°,则∠FOB=6x°,
∵∠BOD=∠AOC=x°,
又∵∠BOF-∠BOD=∠FOD=90°,
∴6x-x=90,
∴x=18
∴∠BOF=6x=108°,
∴∠AOF=180°-108°=72°.
∴∠COE=2∠AOF+∠AOC=2×72+18=162°;
(4)射线OD与OF互相垂直.理由如下:
∵OF,OD分别是∠AOE,∠BOE的平分线,
∴∠DOF=∠DOE+∠EOF=
∠BOE+
∠EOA=
(∠BOE+∠EOA)=
×180°=90°.
∴OD⊥OF.
即射线OD、OF的位置关系是垂直.
(2)∠DOE的所有补角:∠COE、∠AOD;

(3)设∠AOC=x°,则∠FOB=6x°,
∵∠BOD=∠AOC=x°,
又∵∠BOF-∠BOD=∠FOD=90°,
∴6x-x=90,
∴x=18
∴∠BOF=6x=108°,
∴∠AOF=180°-108°=72°.
∴∠COE=2∠AOF+∠AOC=2×72+18=162°;
(4)射线OD与OF互相垂直.理由如下:
∵OF,OD分别是∠AOE,∠BOE的平分线,
∴∠DOF=∠DOE+∠EOF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴OD⊥OF.
即射线OD、OF的位置关系是垂直.
点评:本题考查了角平分线、补角、垂线的定义以及角的计算,属于基础题型,比较简单.

练习册系列答案
相关题目
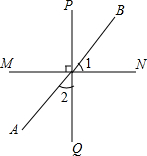 如图,直线PQ⊥MN,垂足为O,AB是过点O的直线,∠1=50°,则∠2的度数为( )
如图,直线PQ⊥MN,垂足为O,AB是过点O的直线,∠1=50°,则∠2的度数为( )| A、50° | B、40° |
| C、60° | D、70° |
 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,若∠B=60°,则∠1的度数是( )
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,若∠B=60°,则∠1的度数是( )| A、15° | B、25° |
| C、10° | D、20° |
 如图,∠AOB=68°,OC平分∠AOB,则∠BOC的度数为
如图,∠AOB=68°,OC平分∠AOB,则∠BOC的度数为 如图,△ABC中,∠ACB=90°,CD是高,AC=8,CB=6,AB=10,求:
如图,△ABC中,∠ACB=90°,CD是高,AC=8,CB=6,AB=10,求: