题目内容
 如图,已知AB是OD的直径,AM和BN是⊙O的两条切线,点E是⊙O上一点,点D是AM上一点,连接DE并延长交BN于点C,连接OD、BE,且OD∥BE.
如图,已知AB是OD的直径,AM和BN是⊙O的两条切线,点E是⊙O上一点,点D是AM上一点,连接DE并延长交BN于点C,连接OD、BE,且OD∥BE.(1)求证:DE是⊙O的切线;
(2)若AD=l,BC=4,求直径AB的长.
考点:切线的判定与性质,全等三角形的判定与性质,勾股定理
专题:计算题
分析:(1)连接OE,由OE=OB,利用等边对等角得到一对角相等,再由OD与BE平行,得到一对同位角及一对内错角相等,等量代换得到∠AOD=∠OBE=∠OEB=∠EOD,再由OA=OE,OD=OD,利用SAS得到三角形AOD与三角形EOD全等,由全等三角形对应角相等得到∠OAD=∠OED,根据AM为圆O的切线,利用切线的性质得到∠OAD=∠OED=90°,即可得证;
(2)过点D作BC的垂线,垂足为H,由BN与圆O切线于点B,得到∠ABC=90°=∠BAD=∠BHD,利用三个角为直角的四边形为矩形得到ADHB为矩形,利用矩形的对边相等得到BH=AD=1,AB=DH,由BC-BH求出HC的长,AD、CB、CD分别切⊙O于点A、B、E,利用切线长定理得到AD=DE=1,EC=BC=4,在直角三角形DHC中,利用勾股定理求出DH的长,即为AB的长.
(2)过点D作BC的垂线,垂足为H,由BN与圆O切线于点B,得到∠ABC=90°=∠BAD=∠BHD,利用三个角为直角的四边形为矩形得到ADHB为矩形,利用矩形的对边相等得到BH=AD=1,AB=DH,由BC-BH求出HC的长,AD、CB、CD分别切⊙O于点A、B、E,利用切线长定理得到AD=DE=1,EC=BC=4,在直角三角形DHC中,利用勾股定理求出DH的长,即为AB的长.
解答: (1)证明:连接OE,
(1)证明:连接OE,
在⊙O中,OA=OE=OB,
∴∠OBE=∠OEB,
∵OD∥BE,
∴∠AOD=∠OBE=∠OEB=∠EOD,
在△AOD和△EOD中,
,
∴△AOD≌△EOD(SAS),
∴∠OAD=∠OED,
∵AM是⊙O的切线,切点为A,
∴BA⊥AM,
∴∠OAD=∠OED=90°,
∴OE⊥DE,
∵OE是⊙O的半径,
∴DE是⊙O的切线;
(2)解:过点D作BC的垂线,垂足为H,
∵BN切⊙O于点B,
∴∠ABC=90°=∠BAD=∠BHD,
∴四边形ABHD是矩形,
∴AD=BH=1,AB=DH,
∴CH=BC-BH=4-1=3,
∵AD、CB、CD分别切⊙O于点A、B、E,
∴AD=ED=1,BC=CE=4,
∴DC=DE+CE=1+4=5,
在Rt△DHC中,DC2=DH2+CH2,
∴AB=DH=
=4.
 (1)证明:连接OE,
(1)证明:连接OE,在⊙O中,OA=OE=OB,
∴∠OBE=∠OEB,
∵OD∥BE,
∴∠AOD=∠OBE=∠OEB=∠EOD,
在△AOD和△EOD中,
|
∴△AOD≌△EOD(SAS),
∴∠OAD=∠OED,
∵AM是⊙O的切线,切点为A,
∴BA⊥AM,
∴∠OAD=∠OED=90°,
∴OE⊥DE,
∵OE是⊙O的半径,
∴DE是⊙O的切线;
(2)解:过点D作BC的垂线,垂足为H,
∵BN切⊙O于点B,
∴∠ABC=90°=∠BAD=∠BHD,
∴四边形ABHD是矩形,
∴AD=BH=1,AB=DH,
∴CH=BC-BH=4-1=3,
∵AD、CB、CD分别切⊙O于点A、B、E,
∴AD=ED=1,BC=CE=4,
∴DC=DE+CE=1+4=5,
在Rt△DHC中,DC2=DH2+CH2,
∴AB=DH=
| 52-32 |
点评:此题考查了切线的判定与性质,全等三角形的判定与性质,以及勾股定理,熟练掌握切线的判定与性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,△ABC中,D是BC上一点,且∠BAD=∠CAE,DE交AC于点F,要证明:△ABC∽△ADE.
如图,△ABC中,D是BC上一点,且∠BAD=∠CAE,DE交AC于点F,要证明:△ABC∽△ADE. 如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=
如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB= 如图,在△ABC中,D是BC边上的中点,∠BDE=∠CDF,请你添加一个条件(不再添加其它线段,不再标注或使用其他字母),使DE=DF成立.
如图,在△ABC中,D是BC边上的中点,∠BDE=∠CDF,请你添加一个条件(不再添加其它线段,不再标注或使用其他字母),使DE=DF成立. 如图,一次函数y=x+1的图象与x轴交于点A,与y轴交于点B,点P位于第一象限且在直线AB上,以PB为一条直角边作一个等腰直角三角形PBC,其中C点位于直线AB的左上方,B点为直角顶点,PC与y轴交于点D.若△PBC与△AOB的面积相等,试求点P的坐标.
如图,一次函数y=x+1的图象与x轴交于点A,与y轴交于点B,点P位于第一象限且在直线AB上,以PB为一条直角边作一个等腰直角三角形PBC,其中C点位于直线AB的左上方,B点为直角顶点,PC与y轴交于点D.若△PBC与△AOB的面积相等,试求点P的坐标. 在锐角三角形ABC中,BC=5,sinA=
在锐角三角形ABC中,BC=5,sinA=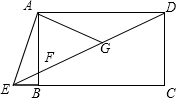 如图,四边形ABCD是矩形,点E在线段CB延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=
如图,四边形ABCD是矩形,点E在线段CB延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=