题目内容
10. 如图,已知点B,E,C,F在同一直线上,AB=DE,AC=DF,BE=CF.求证:AC∥DF.
如图,已知点B,E,C,F在同一直线上,AB=DE,AC=DF,BE=CF.求证:AC∥DF.
分析 根据BE=CF得:BC=EF,由SSS证明△ABC和△DEF(SSS),得∠F=∠ACB,可以得出结论AC∥DF.
解答 证明:∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF,
在△ABC和△DEF中,
∵$\left\{\begin{array}{l}{AB=DE}\\{AC=DF}\\{BC=EF}\end{array}\right.$,
∴△ABC≌△DEF(SSS),
∴∠F=∠ACB,
∴AC∥DF.
点评 本题考查了全等三角形的性质和判定,属于常考题型;熟练掌握全等三角形的判定方法是关键,在应用全等三角形的判定时,要注意三角形间的公共边和公共角,还要注意已知的边或角是否为所要证明的三角形的边或角,如果不是要加以证明,必要时添加适当辅助线构造三角形.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
1.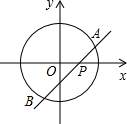 如图,在平面直角坐标系中,已知⊙O的半径为2,动直线AB与x轴交于点P(x,0),直线AB与x轴正方向夹角为45°,若直线AB与⊙O有公共点,则x的取值范围是( )
如图,在平面直角坐标系中,已知⊙O的半径为2,动直线AB与x轴交于点P(x,0),直线AB与x轴正方向夹角为45°,若直线AB与⊙O有公共点,则x的取值范围是( )
 如图,在平面直角坐标系中,已知⊙O的半径为2,动直线AB与x轴交于点P(x,0),直线AB与x轴正方向夹角为45°,若直线AB与⊙O有公共点,则x的取值范围是( )
如图,在平面直角坐标系中,已知⊙O的半径为2,动直线AB与x轴交于点P(x,0),直线AB与x轴正方向夹角为45°,若直线AB与⊙O有公共点,则x的取值范围是( )| A. | -2≤x≤2 | B. | -2$\sqrt{2}$<x<2$\sqrt{2}$ | C. | 0≤x≤2$\sqrt{2}$ | D. | -2$\sqrt{2}$≤x≤2$\sqrt{2}$ |
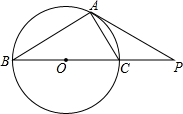 如图,P是⊙O外一点,PA切⊙O于点A,直线PO交⊙O于B,C两点.已知PC=2,AP=2$\sqrt{3}$.求:
如图,P是⊙O外一点,PA切⊙O于点A,直线PO交⊙O于B,C两点.已知PC=2,AP=2$\sqrt{3}$.求: 如图,AB,CD是圆O的直径,且AB⊥CD,P为CD延长线上一点,PE切圆O于E,BE交CD于F,AB=6cm,PE=4cm,则EF的长为$\frac{4\sqrt{10}}{5}$cm.
如图,AB,CD是圆O的直径,且AB⊥CD,P为CD延长线上一点,PE切圆O于E,BE交CD于F,AB=6cm,PE=4cm,则EF的长为$\frac{4\sqrt{10}}{5}$cm. 如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点.当它靠在另一侧墙上时,梯子的顶端在D点,已知梯子长2.5m,D点到地面的垂直距离DE=1.5m,两墙的距离CE长3.5m.求B点到地面的垂直距离BC.
如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点.当它靠在另一侧墙上时,梯子的顶端在D点,已知梯子长2.5m,D点到地面的垂直距离DE=1.5m,两墙的距离CE长3.5m.求B点到地面的垂直距离BC.