Question

20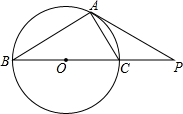．如图，P是⊙O外一点，PA切⊙O于点A，直线PO交⊙O于B，C两点．已知PC=2，AP=2$\sqrt{3}$．求：
（1）⊙O的半径．
（2）AC和AB的长．

Answer 1

分析 （1）连接OA，设半径为r，表示出OP，根据PA为圆的切线，得到OA与AP垂直，在直角三角形AOP中，利用勾股定理列出关于r的方程，求出方程的解即可得到圆的半径；
（2）在直角三角形AOP中，利用直角边等于斜边的一半确定出∠P=30°，进而求出∠AOC=60°，得到三角形AOC为等边三角形，求出AC的长，再由BC为直径得到三角形ABC为直角三角形，利用勾股定理求出AB的长即可．

解答 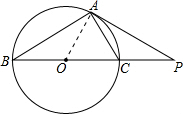解：（1）连接OA，设OA=OC=r，则有OP=OC+CP=r+2，
∵PA为圆O的切线，
∴PA⊥OA，
在Rt△AOP中，根据勾股定理得：OP²=OA²+AP²，即（r+2）²=r²+（2$\sqrt{3}$）²，
解得：r=2，
则圆O的半径为2；
（2）在Rt△AOP中，OA=2，OP=2+2=4，
∴∠P=30°，∠AOC=60°，
∵OA=OC，
∴△AOC为等边三角形，即OC=OA=AC=2，
∵BC为圆O的直径，
∴BA⊥AC，
在Rt△ABC中，AC=2，BC=4，
根据勾股定理得：AB=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$．

点评 此题考查了切线的性质，勾股定理，圆周角定理，以及等边三角形的判定与性质，熟练掌握定理及性质是解本题的关键．