Question

20．同一个圆的内接正方形和内接正六边形的边长之比是$\sqrt{2}$：1．

Answer 1

分析 根据圆内接正方形和正六边形的性质，将问题转化为关于三角形的问题，即可求出正方形和正六边形的边长，进而求出边长之比．

解答 解：如图1，在圆内接正方形ABCD中，OA=OD=R，∠AOD=360°×$\frac{1}{4}$=90°，

则内接正方形的边长为$\frac{R}{sin45°}$=$\sqrt{2}$R；
如图2，在圆内接正六边形ABCDEF中，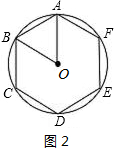

∠AOB=60°，
△AOB为正三角形，
则内接正六边形的边长为R，
所以其比为$\sqrt{2}$：1．
故答案为$\sqrt{2}$：1．

点评 本题考查了正多边形和圆，掌握基本的图形变换．找出内接正方形与外切正六边形的边长关系，是解决问题的关键．