ĚâÄżÄÚČÝ
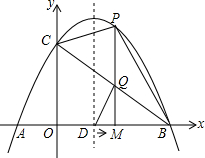 ČçÍĽŁ¬ŇŃÖŞĹ×ÎďĎßy=-x2+3x+4µÄÍĽĎóÓëxÖá˝»ÓÚAˇ˘BÁ˝µăŁ¬ÓëyÖá˝»ÓÚµăCŁ¬Ĺ×ÎďĎߵĶԳĆÖáÓëxÖá˝»ÓÚµăDˇ˘µăM´ÓOµăłö·˘Ł¬ŇÔĂżĂë1¸öµĄÎ»ł¤¶ČµÄËٶČĎňBµăÔ˶ŻŁ¨Ô˶Żµ˝BµăÍŁÖąŁ©Ł¬ąýµăM×÷xÖáµÄ´ąĎߣ¬˝»Ĺ×ÎďĎßÓÚµăPŁ¬˝»BCÓëµăQŁ®
ČçÍĽŁ¬ŇŃÖŞĹ×ÎďĎßy=-x2+3x+4µÄÍĽĎóÓëxÖá˝»ÓÚAˇ˘BÁ˝µăŁ¬ÓëyÖá˝»ÓÚµăCŁ¬Ĺ×ÎďĎߵĶԳĆÖáÓëxÖá˝»ÓÚµăDˇ˘µăM´ÓOµăłö·˘Ł¬ŇÔĂżĂë1¸öµĄÎ»ł¤¶ČµÄËٶČĎňBµăÔ˶ŻŁ¨Ô˶Żµ˝BµăÍŁÖąŁ©Ł¬ąýµăM×÷xÖáµÄ´ąĎߣ¬˝»Ĺ×ÎďĎßÓÚµăPŁ¬˝»BCÓëµăQŁ®Ł¨1Ł©ÇóÖ±ĎßBCµÄ˝âÎöĘ˝Ł»
Ł¨2Ł©Éčµ±µăMÔ˶ŻÁËxŁ¨Ă룩ʱŁ¬ËıßĐÎOBPCµÄĂć»ýÎŞSŁ¬ÇóSÓëxµÄşŻĘýąŘϵʽŁ¬˛˘Ö¸łö×Ô±äÁżxµÄȡֵ·¶Î§Ł»
Ł¨3Ł©ÔÚĎ߶ÎBCÉĎĘÇ·ń´ćÔÚµăQŁ¬ĘąµĂˇ÷DBQłÉÎŞµČŃüČý˝ÇĐÎŁżČô´ćÔÚŁ¬ÇółöµăQµÄ×ř±ęŁ»Čô˛»´ćÔÚŁ¬ËµĂ÷ŔíÓÉŁ®
żĽµăŁş¶ţ´ÎşŻĘý×ŰşĎĚâ
רĚ⣺
·ÖÎöŁşŁ¨1Ł©ŇŃÖŞĹ×ÎďĎß˝âÎöĘ˝Ł¬Áîy=0Ł¬x=0Ł¬żÉÇóBˇ˘CÁ˝µă×ř±ęŁ¬Č»şó¸ůľÝ´ý¶¨ĎµĘý·¨Ľ´żÉÇóµĂŁ»
Ł¨2Ł©ÉčµăPµÄ×ř±ęÎŞPŁ¨xŁ¬yŁ©Ł¬ÓÉSËıßĐÎOBPC=Sˇ÷OPC+Sˇ÷OPBżÉÁĐłöSÓëxµÄşŻĘýąŘϵʽŁ¬ÓÉÓÚBŁ¨4Ł¬0Ł©Ł¬ËůŇÔ0ˇÜxˇÜ4
Ł¨3Ł©ÓĐČýÖÖżÉÄÜŁş˘ŮBQ=DQŁ¬˘ÚBQ=BD=
Ł¬˘ŰDQ=BD=
Ł¬·Ö±đĚÖÂŰĽ´żÉÇóµĂŁ®
Ł¨2Ł©ÉčµăPµÄ×ř±ęÎŞPŁ¨xŁ¬yŁ©Ł¬ÓÉSËıßĐÎOBPC=Sˇ÷OPC+Sˇ÷OPBżÉÁĐłöSÓëxµÄşŻĘýąŘϵʽŁ¬ÓÉÓÚBŁ¨4Ł¬0Ł©Ł¬ËůŇÔ0ˇÜxˇÜ4
Ł¨3Ł©ÓĐČýÖÖżÉÄÜŁş˘ŮBQ=DQŁ¬˘ÚBQ=BD=
| 5 |
| 2 |
| 5 |
| 2 |
˝â´đŁş˝âŁşŁ¨1Ł©°Ńx=0´úČëy=-x2+3x+4µĂµăCµÄ×ř±ęÎŞCŁ¨0Ł¬4Ł©
°Ńy=0´úČëy=-x2+3x+4µĂµăBµÄ×ř±ęÎŞBŁ¨4Ł¬0Ł©
ÉčÖ±ĎßBCµÄ˝âÎöʽΪy=kx+bŁ¨kˇŮ0Ł©Ł¬
ˇŕ
Ł¬˝âµĂ
Ł¬
ˇŕÖ±ĎßBCµÄ˝âÎöʽΪy=-x+4Ł»
Ł¨2Ł©ČçÍĽŁ¬Á¬˝ÓOPŁ¬ÉčµăPµÄ×ř±ęÎŞPŁ¨xŁ¬yŁ©
SËıßĐÎOBPC=Sˇ÷OPC+Sˇ÷OPB=
ˇÁ4ˇÁx+
ˇÁ4ˇÁy
=2x+2y
=2x+2Ł¨-x2+3x+4Ł©
=-2x2+8x+8Ł®
ˇßµăMÔ˶Żµ˝BµăÉĎÍŁÖąŁ¬
ˇŕ0ˇÜxˇÜ4
ˇŕS=-2x2+8x+8Ł¨0ˇÜxˇÜ4Ł©
Ł¨3Ł©´ćÔÚŁ®
ˇßy=-x2+3x+4=-Ł¨x-
Ł©2+
Ł¬
ˇŕ¶ĄµăµÄ×ř±ęÎŞŁ¨
Ł¬
Ł©Ł¬
ˇßOB=OC=4Ł¬
ˇŕBC=
=4
Ł¬ˇĎABC=45ˇăŁ¬
˘ŮČôBQ=DQ
ˇßBQ=DQŁ¬BD=4-
=
Ł¬
ˇŕBM=QM=
Ł¬
ˇŕOM=4-
=
Ł¬
ËůŇÔQµÄ×ř±ęÎŞQŁ¨
Ł¬
Ł©Ł®
˘ÚČôBQ=BD=
ˇßˇ÷BQMˇ×ˇ÷BCOŁ¬
ˇŕ
=
=
Ł¬
ˇŕ
=
=
Ł¬
ˇŕQM=BM=
Ł¬
ˇŕOM=4-
Ł¬
ËůŇÔQµÄ×ř±ęÎŞQŁ¨4-
Ł¬
Ł©Ł®
˘ŰČôDQ=BD=
Ł¬
ˇßˇĎABC=45ˇăŁ¬
ˇŕDQˇÍBDŁ¬
ˇŕˇ÷BDQĘǵČŃüÖ±˝ÇČý˝ÇĐÎŁ¬
ˇŕDQ=BD=
Ł¬
ËůŇÔQµÄ×ř±ęÎŞQŁ¨
Ł¬
Ł©Ł¬
×ŰÉĎËůĘöŁ¬QµÄ×ř±ęÎŞQŁ¨
Ł¬
Ł©»ňQŁ¨4-
Ł¬
Ł©»ňQŁ¨
Ł¬
Ł©Ł®
°Ńy=0´úČëy=-x2+3x+4µĂµăBµÄ×ř±ęÎŞBŁ¨4Ł¬0Ł©
ÉčÖ±ĎßBCµÄ˝âÎöʽΪy=kx+bŁ¨kˇŮ0Ł©Ł¬
ˇŕ
|
|
ˇŕÖ±ĎßBCµÄ˝âÎöʽΪy=-x+4Ł»
Ł¨2Ł©ČçÍĽŁ¬Á¬˝ÓOPŁ¬ÉčµăPµÄ×ř±ęÎŞPŁ¨xŁ¬yŁ©

SËıßĐÎOBPC=Sˇ÷OPC+Sˇ÷OPB=
| 1 |
| 2 |
| 1 |
| 2 |
=2x+2y
=2x+2Ł¨-x2+3x+4Ł©
=-2x2+8x+8Ł®
ˇßµăMÔ˶Żµ˝BµăÉĎÍŁÖąŁ¬
ˇŕ0ˇÜxˇÜ4
ˇŕS=-2x2+8x+8Ł¨0ˇÜxˇÜ4Ł©
Ł¨3Ł©´ćÔÚŁ®
ˇßy=-x2+3x+4=-Ł¨x-
| 3 |
| 2 |
| 25 |
| 4 |
ˇŕ¶ĄµăµÄ×ř±ęÎŞŁ¨
| 3 |
| 2 |
| 25 |
| 4 |
ˇßOB=OC=4Ł¬
ˇŕBC=
| OB2+OC2 |
| 2 |
˘ŮČôBQ=DQ
ˇßBQ=DQŁ¬BD=4-
| 3 |
| 2 |
| 5 |
| 2 |
ˇŕBM=QM=
| 5 |
| 4 |
ˇŕOM=4-
| 5 |
| 4 |
| 11 |
| 4 |
ËůŇÔQµÄ×ř±ęÎŞQŁ¨
| 11 |
| 4 |
| 5 |
| 4 |
˘ÚČôBQ=BD=
| 5 |
| 2 |
ˇßˇ÷BQMˇ×ˇ÷BCOŁ¬
ˇŕ
| BQ |
| BC |
| QM |
| CO |
| BM |
| BO |
ˇŕ
| ||
4
|
| QM |
| 4 |
| BM |
| 4 |
ˇŕQM=BM=
5
| ||
| 4 |
ˇŕOM=4-
5
| ||
| 4 |
ËůŇÔQµÄ×ř±ęÎŞQŁ¨4-
5
| ||
| 4 |
5
| ||
| 4 |
˘ŰČôDQ=BD=
| 5 |
| 2 |
ˇßˇĎABC=45ˇăŁ¬
ˇŕDQˇÍBDŁ¬
ˇŕˇ÷BDQĘǵČŃüÖ±˝ÇČý˝ÇĐÎŁ¬
ˇŕDQ=BD=
| 5 |
| 2 |
ËůŇÔQµÄ×ř±ęÎŞQŁ¨
| 3 |
| 2 |
| 5 |
| 2 |
×ŰÉĎËůĘöŁ¬QµÄ×ř±ęÎŞQŁ¨
| 11 |
| 4 |
| 5 |
| 4 |
5
| ||
| 4 |
5
| ||
| 4 |
| 3 |
| 2 |
| 5 |
| 2 |
µăĆŔŁş±ľĚ⿼˛éÁ˶ţ´ÎşŻĘý˝âÎöĘ˝µÄÔËÓĂŁ¬×ř±ęϵŔďĂć»ý±íĘľ·˝·¨Ł¬Ľ°Ń°ŐŇĚŘĘâČý˝ÇĐεÄĚőĽţÎĘĚ⣬É漰·ÖŔŕĚÖÂŰşÍĎŕËĆČý˝ÇĐεÄÔËÓĂŁ®

Á·Ď°˛áϵÁĐ´đ°¸
ĎŕąŘĚâÄż
 ČçÍĽŁ¬ÔÚˇ÷ABCÖĐŁ¬Á˝ĚőÖĐĎßADˇ˘BE˝»ÓÚµăFŁ¬ÔňSˇ÷EDFŁşSˇ÷ABC=
ČçÍĽŁ¬ÔÚˇ÷ABCÖĐŁ¬Á˝ĚőÖĐĎßADˇ˘BE˝»ÓÚµăFŁ¬ÔňSˇ÷EDFŁşSˇ÷ABC= ČçÍĽŁ¬Ň»¸öÔ˛ÖůŁ¬ËüµÄ¸ßÎŞ20cmŁ¬µ×Ăć°ëľ¶ÎŞ7cmŁ®ČçąűһֻÂěŇĎŇŞ×ÔÔ˛Öůϵ×ĂćµÄAµăŁ¬ŃŘÔ˛ÖůĚĺµÄ˛ŕĂćĹŔµ˝ÓëAĎŕ¶ÔµÄÉϵ×ĂćBµăŁ¬ÇóĹŔĐеÄ×î¶Ěł¤¶ČŁ¨˝áąű±ŁÁô¦ĐŁ©Ł®
ČçÍĽŁ¬Ň»¸öÔ˛ÖůŁ¬ËüµÄ¸ßÎŞ20cmŁ¬µ×Ăć°ëľ¶ÎŞ7cmŁ®ČçąűһֻÂěŇĎŇŞ×ÔÔ˛Öůϵ×ĂćµÄAµăŁ¬ŃŘÔ˛ÖůĚĺµÄ˛ŕĂćĹŔµ˝ÓëAĎŕ¶ÔµÄÉϵ×ĂćBµăŁ¬ÇóĹŔĐеÄ×î¶Ěł¤¶ČŁ¨˝áąű±ŁÁô¦ĐŁ©Ł® ČçÍĽŁ¬ÔÚÖ±˝ÇĚÝĐÎABCDÖĐŁ¬ADˇÎBCŁ¬ˇĎBAD=90ˇăŁ¬AB=4Ł¬CD=5Ł¬AD=6Ł¬¶ŻµăP´ÓµăAżŞĘĽŇÔĂżĂë1¸öµĄÎ»ł¤¶ČµÄËٶČĎňµăBÔČËŮÔ˶ŻŁ¬¶ŻµăQ´ÓµăBżŞĘĽŃŘŐŰĎßBC-CDŇÔĂżĂë2¸öµĄÎ»ł¤¶ČµÄËٶČĎňµăDÔČËŮÔ˶ŻŁ¬ąýµăP×÷PEˇÍABŁ¬˝»CDÓÚµăEŁ¬ÉčµăPˇ˘QͬʱżŞĘĽÔ˶ŻŁ¬ÇŇʱĽäÎŞtĂ루tŁľ0Ł©Ł¬µ±µăPÓëµăBÖŘşĎʱֹͣÔ˶ŻŁ¬µăQҲËćֹ֮ͣÔ˶ŻŁ®
ČçÍĽŁ¬ÔÚÖ±˝ÇĚÝĐÎABCDÖĐŁ¬ADˇÎBCŁ¬ˇĎBAD=90ˇăŁ¬AB=4Ł¬CD=5Ł¬AD=6Ł¬¶ŻµăP´ÓµăAżŞĘĽŇÔĂżĂë1¸öµĄÎ»ł¤¶ČµÄËٶČĎňµăBÔČËŮÔ˶ŻŁ¬¶ŻµăQ´ÓµăBżŞĘĽŃŘŐŰĎßBC-CDŇÔĂżĂë2¸öµĄÎ»ł¤¶ČµÄËٶČĎňµăDÔČËŮÔ˶ŻŁ¬ąýµăP×÷PEˇÍABŁ¬˝»CDÓÚµăEŁ¬ÉčµăPˇ˘QͬʱżŞĘĽÔ˶ŻŁ¬ÇŇʱĽäÎŞtĂ루tŁľ0Ł©Ł¬µ±µăPÓëµăBÖŘşĎʱֹͣÔ˶ŻŁ¬µăQҲËćֹ֮ͣÔ˶ŻŁ®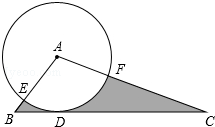 ČçÍĽŁ¬ÔÚˇ÷ABCÖĐŁ¬BC=6Ł¬ŇÔµăAÎŞÔ˛ĐÄŁ¬2ÎŞ°ëľ¶µÄˇŃAÓëBCĎŕÇĐÓÚµăDŁ¬˝»ABÓÚµăEŁ¬˝»ACÓÚµăFŁ¬ˇĎEAF=120ˇăŁ¬ÔňÍĽÖĐŇőÓ°˛ż·ÖµÄĂć»ýĘÇ
ČçÍĽŁ¬ÔÚˇ÷ABCÖĐŁ¬BC=6Ł¬ŇÔµăAÎŞÔ˛ĐÄŁ¬2ÎŞ°ëľ¶µÄˇŃAÓëBCĎŕÇĐÓÚµăDŁ¬˝»ABÓÚµăEŁ¬˝»ACÓÚµăFŁ¬ˇĎEAF=120ˇăŁ¬ÔňÍĽÖĐŇőÓ°˛ż·ÖµÄĂć»ýĘÇ