题目内容
 如图,在△ABC中,两条中线AD、BE交于点F,则S△EDF:S△ABC=
如图,在△ABC中,两条中线AD、BE交于点F,则S△EDF:S△ABC=考点:三角形的面积,三角形的角平分线、中线和高
专题:
分析:先根据AD、BE是△ABC的中线得出DE∥AB,DE=
AB,S△ACD=S△ABD,再由相似三角形的判定定理得出△DEF∽△AFB,由相似三角形的性质可得出两三角形面积的比,设S△DEF=x,用x表示出各三角形的面积,进而可得出结论.
| 1 |
| 2 |
解答:解:∵AD、BE是△ABC的中线,
∴DE∥AB,DE=
AB,S△ACD=S△ABD,
∴∠FDE=∠FAB,∠AFB=∠DFE,
∴△DEF∽△AFB,
∴
=
=
=
,
∴
=
,
∴设S△DEF=x,则S△ABF=4x,S△AEF=S△BDF=2x,
∵S△ACD=S△ABD,
∴S△DCE=3x,
∴S△EDF:S△ABC=x:12x=1:12.
故答案为:1:12.
∴DE∥AB,DE=
| 1 |
| 2 |
∴∠FDE=∠FAB,∠AFB=∠DFE,
∴△DEF∽△AFB,
∴
| DF |
| AF |
| EF |
| BF |
| DE |
| AB |
| 1 |
| 2 |
∴
| S△DEF |
| S△ABF |
| 1 |
| 4 |
∴设S△DEF=x,则S△ABF=4x,S△AEF=S△BDF=2x,
∵S△ACD=S△ABD,
∴S△DCE=3x,
∴S△EDF:S△ABC=x:12x=1:12.
故答案为:1:12.
点评:本题考查的是三角形的面积,熟知三角形的中线把三角形的面积分为相等的两部分是解答此题的关键.

练习册系列答案
相关题目
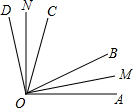 如图所示,OB、OC是∠AOD内的任意两条射线,OM平分∠AOB,ON平分∠COD.若∠AOD=120°,∠BOC=70°.求∠MON使多少度?
如图所示,OB、OC是∠AOD内的任意两条射线,OM平分∠AOB,ON平分∠COD.若∠AOD=120°,∠BOC=70°.求∠MON使多少度?
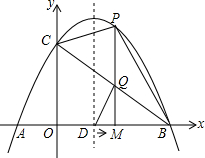 如图,已知抛物线y=-x2+3x+4的图象与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴与x轴交于点D、点M从O点出发,以每秒1个单位长度的速度向B点运动(运动到B点停止),过点M作x轴的垂线,交抛物线于点P,交BC与点Q.
如图,已知抛物线y=-x2+3x+4的图象与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴与x轴交于点D、点M从O点出发,以每秒1个单位长度的速度向B点运动(运动到B点停止),过点M作x轴的垂线,交抛物线于点P,交BC与点Q.