题目内容
方程ax2+bx+c=0(a≠0)系数满足a+c=b,方程组
的解为 .
|
考点:解三元一次方程组,一元二次方程的解
专题:
分析:由题意可知:把x=-1代入一元二次方程ax2+bx+c=0(a≠0)中即可得到b=a+c,则据此可以知道方程的根为x=-1,把x=-1代入方程组即可求得y=2,z=4,从而求得方程组的解.
解答:
解:把x=-1代入一元二次方程ax2+bx+c=0(a≠0)中得,
a-b+c=0,
即b=a+c,
所以该方程必定有一个根是:x=-1,
解方程组
得
,
∴方程组
的解为
.
故答案为
.
a-b+c=0,
即b=a+c,
所以该方程必定有一个根是:x=-1,
解方程组
|
|
∴方程组
|
|
故答案为
|
点评:本题考查的是一元二次方程的根以及解三元一次方程组.解该题的关键是分析题意,得出x=-1.

练习册系列答案
相关题目
下面四幅图案中,属于轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
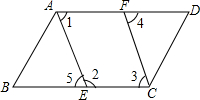 如图,根据图形完成下列填空.
如图,根据图形完成下列填空. 将单项式a,2a2,3a3,4a4按右侧方式排列,若规定(m,n)表示第m排从左向右第n个单项式,如:(3,2)表示的是a,(5,4)表示的是,则(10,1)与(25,7)的积是
将单项式a,2a2,3a3,4a4按右侧方式排列,若规定(m,n)表示第m排从左向右第n个单项式,如:(3,2)表示的是a,(5,4)表示的是,则(10,1)与(25,7)的积是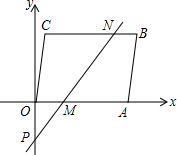 如图,在平面直角坐标系中,四边形OABC为平行四边形,A(5,0),C(1,4),过点P(0,-2)的直线分别交OA、BC于M、N,且将?OABC的面积分成相等的两部分,求点M,N的坐标.
如图,在平面直角坐标系中,四边形OABC为平行四边形,A(5,0),C(1,4),过点P(0,-2)的直线分别交OA、BC于M、N,且将?OABC的面积分成相等的两部分,求点M,N的坐标.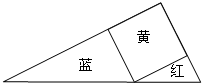 如图所示,用一张斜边长为30cm的红色直角三角形纸片,一张斜边长为50cm的蓝色直角三角形纸片,一张黄色的正方形纸片,恰好能拼成一个直角三角形,问:红、蓝两张三角形纸片的面积之和是多少?
如图所示,用一张斜边长为30cm的红色直角三角形纸片,一张斜边长为50cm的蓝色直角三角形纸片,一张黄色的正方形纸片,恰好能拼成一个直角三角形,问:红、蓝两张三角形纸片的面积之和是多少?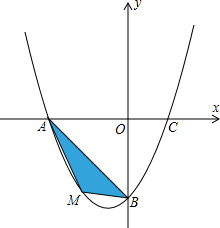 如图,在平面直角坐标系中,抛物线经过A(-4,0)、B(0,-4)、C(2,0)三点.
如图,在平面直角坐标系中,抛物线经过A(-4,0)、B(0,-4)、C(2,0)三点.