题目内容
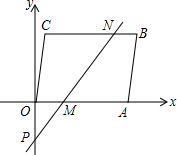 如图,在平面直角坐标系中,四边形OABC为平行四边形,A(5,0),C(1,4),过点P(0,-2)的直线分别交OA、BC于M、N,且将?OABC的面积分成相等的两部分,求点M,N的坐标.
如图,在平面直角坐标系中,四边形OABC为平行四边形,A(5,0),C(1,4),过点P(0,-2)的直线分别交OA、BC于M、N,且将?OABC的面积分成相等的两部分,求点M,N的坐标.考点:平行四边形的性质,一次函数图象上点的坐标特征,待定系数法求一次函数解析式
专题:
分析:因为过点P(0,-2)的直线分别交OA、BC于M、N,且将?OABC的面积分成相等的两部分,所以直线MN必过平行四边形的中心W,由A和C的坐标即可求出其中心坐标W,设过直线M、N的解析式为y=kx+b,把W和P的坐标代入即可求出直线解析式,进而可求出M的坐标,因为W的坐标已求出所以N的坐标也可求出.
解答:
解:∵四边形OABC为平行四边形,A(5,0),C(1,4),
∴其中心对称点W坐标为(3,2);
设过直线M、N的解析式为y=kx+b,把W和P的坐标代入得:
,
解得:k=
,b=-2,
∴y=
x-2,
设y=0,则x=1.5,
∴点M的坐标为(1.5,0),
∵W坐标为(3,2),
∴N的坐标为(4.5,4).
∴其中心对称点W坐标为(3,2);
设过直线M、N的解析式为y=kx+b,把W和P的坐标代入得:

|
解得:k=
| 4 |
| 3 |
∴y=
| 4 |
| 3 |
设y=0,则x=1.5,
∴点M的坐标为(1.5,0),
∵W坐标为(3,2),
∴N的坐标为(4.5,4).
点评:此题考查了平行四边形的性质、坐标与图形性质以及利用待定系数法求一次函数的解析式,解题的关键是求出其中心对称点的坐标.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
下列各数中,界于4和5之间的一个是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列斜坡最陡的是( )
A、斜坡AB的坡度为
| ||
| B、斜坡CD的倾斜角是45° | ||
| C、斜坡EF的坡比为1:3 | ||
D、斜坡GH的坡角为α,tanα=
|
分式
,
,
的最简公分母是( )
| 1 |
| a2-2a+1 |
| 1 |
| a2-1 |
| 1 |
| a2+2a+1 |
| A、a4+2a2+1 |
| B、(a2-1)(a2+1) |
| C、a4-2a2+1 |
| D、(a-1)4 |
若(2y+1)2+|x-
|=0,则x2+y2的值是( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
 有一位滑翔伞爱好者,正在空中匀速向下滑翔,已知水平方向上的风速为5.8m/s,如图,在A点他观察到C处塔尖的俯角为30°,5s后在B点的他观察到C处塔尖的俯角为45°,此时,塔尖与他本人的距离BC是AC的
有一位滑翔伞爱好者,正在空中匀速向下滑翔,已知水平方向上的风速为5.8m/s,如图,在A点他观察到C处塔尖的俯角为30°,5s后在B点的他观察到C处塔尖的俯角为45°,此时,塔尖与他本人的距离BC是AC的
 画出如图所示立体图形的三视图.
画出如图所示立体图形的三视图.