题目内容
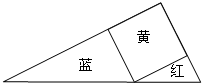 如图所示,用一张斜边长为30cm的红色直角三角形纸片,一张斜边长为50cm的蓝色直角三角形纸片,一张黄色的正方形纸片,恰好能拼成一个直角三角形,问:红、蓝两张三角形纸片的面积之和是多少?
如图所示,用一张斜边长为30cm的红色直角三角形纸片,一张斜边长为50cm的蓝色直角三角形纸片,一张黄色的正方形纸片,恰好能拼成一个直角三角形,问:红、蓝两张三角形纸片的面积之和是多少?考点:相似三角形的应用
专题:
分析:首先利用相似三角形的判定方法得出△ADC∽△CEB,进而表出DC,BE的长,再利用勾股定理求出即可.
解答:
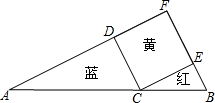 解:∵∠ACD+∠BCE=90°,∠B+∠ECB=90°,
解:∵∠ACD+∠BCE=90°,∠B+∠ECB=90°,
∴∠ACD=∠B,
∵∠ADC=∠CEB=90°,
∴△ADC∽△CEB,
∴
=
=
=
,
设DC=x,则EC=x,BE=
x,
故x2+(
x)2=302,
解得:x2=
,
故红、蓝两张三角形纸片的面积之和是:
DC×AD+
EB×EC=
(x×
x+x×
x)=
×(
+
)×
=750.
 解:∵∠ACD+∠BCE=90°,∠B+∠ECB=90°,
解:∵∠ACD+∠BCE=90°,∠B+∠ECB=90°,∴∠ACD=∠B,
∵∠ADC=∠CEB=90°,
∴△ADC∽△CEB,
∴
| AC |
| BC |
| DC |
| BE |
| AD |
| EC |
| 5 |
| 3 |
设DC=x,则EC=x,BE=
| 3 |
| 5 |
故x2+(
| 3 |
| 5 |
解得:x2=
| 11250 |
| 17 |
故红、蓝两张三角形纸片的面积之和是:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 3 |
| 3 |
| 5 |
| 1 |
| 2 |
| 5 |
| 3 |
| 3 |
| 5 |
| 11250 |
| 17 |
点评:此题主要考查了相似三角形的应用,求出x2的值是解题关键.

练习册系列答案
相关题目
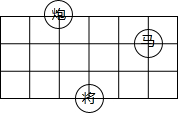 如图,象棋盘(部分)中,若“马”位置用(0,0)表示,“炮”的位置用(-3,1)表示,则“将”的位置表示为( )
如图,象棋盘(部分)中,若“马”位置用(0,0)表示,“炮”的位置用(-3,1)表示,则“将”的位置表示为( )| A、(0,0) |
| B、(-2,-2) |
| C、(0,-2) |
| D、(-2,-3) |
下列方程中,属于一元二次方程的是( )
| A、(x+6)2=16 | ||
| B、x2+3x=16+x2 | ||
| C、xy=16 | ||
D、x2-
|
某车间原计划每天生产50个零件,改进技术后,每天比原计划多生产6个,结果提前3天并超额完成120个零件.若设原计划需生产x个零件,则可列方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
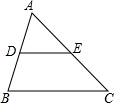 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠C=40°.
如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠C=40°.