题目内容
19．设x1、x2是方程x2-2x-m=0的两根，且2x1+x2=0，则m的值是8．分析 先根据根与系数的关系得到x1+x2=2，x1x2=-m，再利用2x1+x2=0可求出x1=2，x2=-4，然后计算m的值．
解答 解：根据题意得，x1+x2=2，x1x2=-m，
而2x1+x2=0，
所以x1=2，则x2=-4，
所以-m=2×（-4），
解得m=8．
故答案为8．
点评 本题考查根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．
练习册系列答案
相关题目
9．把（2-x）$\sqrt{\frac{1}{x-2}}$的根号外的（2-x）移入根号内得（ ）
| A． | $\sqrt{2-x}$ | B． | $\sqrt{x-2}$ | C． | -$\sqrt{2-x}$ | D． | -$\sqrt{x-2}$ |
如图，已知D为△ABC边BC延长线上一点，DF⊥AB于F交AC于E，∠A=35°，∠D=42°，则∠ACD的度数为83°．
14．下列各式计算正确的是（ ）
| A． | （-2$\sqrt{3}$）2=6 | B． | $\sqrt{1\frac{25}{49}}$=1$\frac{5}{7}$ | ||
| C． | $\sqrt{（-121）×（-9）}$=$\sqrt{121}$×$\sqrt{9}$=33 | D． | $\sqrt{（-4）^{2}}$=±4 |
4．整数m满足$\left\{\begin{array}{l}{2m-1＞0}\\{4-2m＞-1}\end{array}\right.$，则关于x的方程m2x2-4x-2=（m+2）x2+3x+4的解为（ ）
| A． | x1=-2，x2=-$\frac{3}{2}$ | B． | x1=2，x2=$\frac{3}{2}$ | ||
| C． | x1=-$\frac{6}{7}$ | D． | x1=-2，x2=-$\frac{3}{2}$，x3=-$\frac{6}{7}$ |
11．两个不等的实数a、b满足a2+a-1=0，b2+b-1=0，则ab的值为（ ）
| A． | 1 | B． | -1 | C． | $\frac{{-1±\sqrt{5}}}{2}$ | D． | $\sqrt{2}$ |
8．下列四组线段中，可以构成直角三角形的是（ ）
| A． | 4，5，6 | B． | 5，12，13 | C． | 2，3，4 | D． | 1，$\sqrt{2}$，3 |
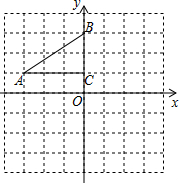如图，在平面直角坐标系中，直角△ABC的三个顶点分别是：A（-3，1），B（0，3），C（0，1）