题目内容
13.在矩形ABCD中,AB=6cm,BC=8cm,点P从点A出发沿AB边以1cm/s的速度向点B移动,同时,点Q从点B出发沿BC以2cm、s的速度向点C移动,其中一点到达终点时,另一点随之停止运功.设运动时间为t秒:(1)如图1,几秒后,△DPQ的面积等于21cm2?
(2)在运动过程中,若以P为圆心的⊙P同时与直线AD、BD相切(如图2),求t值;
(3)若以Q为圆心,PQ为半径作⊙Q.
①在运动过程中,是否存在t值,使得点D落在⊙Q上?若存在,求出t值;若不存在,请说明理由;
②若⊙Q与四边形CDPQ有三个公共点,则t的取值范围为0<t<4.(直接写出结果,不需说理)

分析 (1)由题意可知PA=t,BQ=2t,从而得到PB=6-t,BQ=2t,QC=8-2t,然后依据△DPQ的面积等于21cm2列方程求解即可;
(2)如图1所示:连结PE.依据勾股定理可求得BD的长,然后依据切线长定理可知DE=AD=8,从而可求得BE的长,由圆的半径相等可知PE=AP=t,然后再Rt△PEB中依据勾股定理列方程求解即可;
(3)①如图2所示:先用含t的式子表示出BP、BQ、CQ的长,然后依据DC2+CQ2=PB2+QB2列出关于t的方程,从而可求得t的值;②当t=0时,⊙Q与四边形DPQC有两个公共点,由①可知当t=4时,⊙Q与四边形DPQC有两个公共点,从而可确定出t的取值范围.
解答 解:(1)∵当运动时间为t秒时,PA=t,BQ=2t,
∴PB=6-t,BQ=2t,CQ=8-2t.
∵△DPQ的面积等于21cm2,
∴6×8-$\frac{1}{2}$×8×t-$\frac{1}{2}$(6-t)•2t-$\frac{1}{2}$×6×(8-2t)=21.
整理得:t2-4t+3=0,解得t=1或t=3.
答:当t为1秒或3秒时,△DPQ的面积等于21cm2.
(2)如图1所示:连结PE.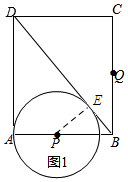
∵⊙P分别与AD、BD相切,
∴PE⊥BD,AD=DE=8.
在Rt△ABD中,依据勾股定理可知BD=10.
∴BE=BD-DE=2.
∵AP=PE,
∴PE=t,PB=6-t.
在Rt△PEB中,依据勾股定理可知:(6-t)2=t2+22,解得:t=$\frac{8}{3}$.
(3)①如图2所示: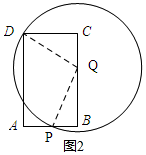
∵PA=t,BQ=2t,
∴PB=6-t,CQ=8-2t.
∵点D在⊙Q上,
∴QD=PQ.
∴DC2+CQ2=PB2+QB2,即62+(8-2t)2=(2t)2+(6-t)2.
整理得:t2+20t-64=0.解得t=4或t=16(舍去).
所以当t=4时,点D落在⊙Q上.
②(Ⅰ)当t=0时,如图3所示: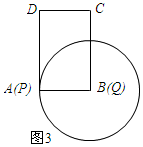
⊙Q与四边形DPQC有两个公共点;
(Ⅱ)如图4所示:当圆Q经过点D时,⊙Q与四边形DPQC有两个公共点.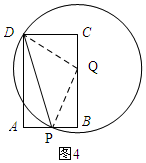
由①可知此时t=4.
∴当0<t<4时,⊙Q与四边形CDPQ有三个公共点.
故答案为:0<t<4.
点评 本题主要考查的是主要考查的是圆的综合应用,解答本题主要应用了三角形的面积公式、切线长定理、勾股定理、圆的性质,依据题意列出关于t的方程是解题的关键.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案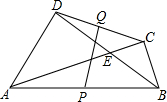 如图,四边形ABCD中,对角线AC与BD相交于点E,∠ADB=∠ACB=90°,P,Q分别是AB,CD的中点,给出下列结论:(1)PQ⊥CD;(2)AB=2PQ;(3)∠ADC与∠ABC互补.其中正确的是( )
如图,四边形ABCD中,对角线AC与BD相交于点E,∠ADB=∠ACB=90°,P,Q分别是AB,CD的中点,给出下列结论:(1)PQ⊥CD;(2)AB=2PQ;(3)∠ADC与∠ABC互补.其中正确的是( )| A. | (1)(2)(3) | B. | (1)(2) | C. | (1)(3) | D. | (2)(3) |
 如图,已知D、E分别是△ABC的边AB、AC的中点,则S△ADE:S四边形DECB=( )
如图,已知D、E分别是△ABC的边AB、AC的中点,则S△ADE:S四边形DECB=( )| A. | 1:2 | B. | 1:3 | C. | 2:3 | D. | 1:4 |
| A. | 2cm,3cm,4cm,6cm | B. | 1cm,$\sqrt{2}$cm,$\sqrt{3}cm$,$\sqrt{6}$cm | C. | 1cm,2cm,3cm,6cm | D. | 1cm,2cm,3cm,5cm |
| A. |  | B. |  | C. |  | D. |  |
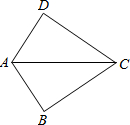 如图,四边形ABCD中,BC=DC,要使△ABC≌△ADC,还需要添加一个条件,你添加的条件是AD=AB或者∠ACD=∠ACB或者∠B=∠D=90°(写一个即可).
如图,四边形ABCD中,BC=DC,要使△ABC≌△ADC,还需要添加一个条件,你添加的条件是AD=AB或者∠ACD=∠ACB或者∠B=∠D=90°(写一个即可).
 如图,在△ABC中,BD是AC边上的中线,E是BC上一点,AE与BD相交于点F.
如图,在△ABC中,BD是AC边上的中线,E是BC上一点,AE与BD相交于点F.