题目内容
14．在一个不透明的箱子里放有4张相同的卡片，分别标有“1”、“2”、“3”、“4”的字样，规定：从箱子里先后摸出两张卡片（每一次摸出后不放回），则摸出两张卡片的数字之和不小于5的概率为$\frac{2}{3}$．分析 首先根据题意画出树状图，然后由树状图求得所有等可能的结果与两次摸出的小球标号的和不小于5的情况，再利用概率公式求解即可求得答案．
解答 解：根据题意画树状图如下：
共有12种情况，两张卡片上的数字之不小于5的有8种，
则这两张卡片上的数字之和不小于5的概率为$\frac{8}{12}$=$\frac{2}{3}$，
故答案为：$\frac{2}{3}$．
点评 此题考查了列表法或树状图法求概率．注意此题是不放回实验．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
浙江之星课时优化作业系列答案
激活思维优加课堂系列答案
相关题目
17．
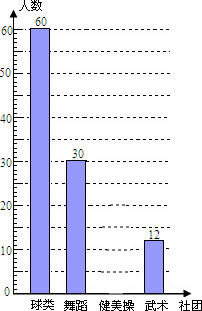为推进“全国亿万学生阳光体育运动”的实施，组织广大同学开展健康向上的第二课堂活动．我市某中学准备组建球类社团（足球、篮球、羽毛球、乒乓球）、舞蹈社团、健美操社团、武术社团，为了解在校学生对这4个社团活动的喜爱情况，该校随机抽取部分初中生进行了“你最喜欢哪个社团”调查，依据相关数据绘制成以下不完整的统计表，请根据图表中的信息解答下列问题：
（1）求样本容量及表格中m、n的值；
（2）请补全统计图；
（3）被调查的60个喜欢球类同学中有3人最喜欢足球，若该校有3000名学生，请估计该校最喜欢足球的人数．
为推进“全国亿万学生阳光体育运动”的实施，组织广大同学开展健康向上的第二课堂活动．我市某中学准备组建球类社团（足球、篮球、羽毛球、乒乓球）、舞蹈社团、健美操社团、武术社团，为了解在校学生对这4个社团活动的喜爱情况，该校随机抽取部分初中生进行了“你最喜欢哪个社团”调查，依据相关数据绘制成以下不完整的统计表，请根据图表中的信息解答下列问题：| 社团类别 | 人数 | 占总人数比例 |
| 球类 | 60 | m |
| 舞蹈 | 30 | 0.25 |
| 健美操 | n | 0.15 |
| 武术 | 12 | 0.1 |
（2）请补全统计图；
（3）被调查的60个喜欢球类同学中有3人最喜欢足球，若该校有3000名学生，请估计该校最喜欢足球的人数．
某企业下属A、B两公司1--4月份销售额如图所示．通过观察，你能比较出A、B两公司销售额的标准差的大小吗？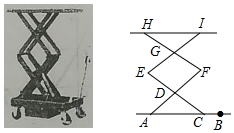
如图是某科技馆展览的一个升降平台模型，在其示意图中，AB=AF=CE=EI=FH=50cm，其中点D是AF和CE的中点，点G是EI和FH的中点．当点C在线段AB上滑动时，∠DAC的大小随之发生变化，平台的高度也随之发生变化，从而控制平台面HI的升降．
4．下列一次函数中，随着增大而减小而的是（ ）
| A． | y=3x | B． | y=3x-2 | C． | y=-3x-2 | D． | y=3+2x |