题目内容
17.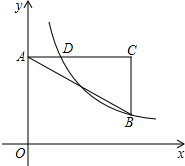 如图在直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B,C的横坐标都是3,且BC=2,点D在AC上且横坐标为1,若反比例函数y=$\frac{k}{x}$(x>0)图象象经过点B,D,求k的值.
如图在直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B,C的横坐标都是3,且BC=2,点D在AC上且横坐标为1,若反比例函数y=$\frac{k}{x}$(x>0)图象象经过点B,D,求k的值.
分析 先根据反比例函数图象上的点的坐标特征表示出点B的坐标,再表示出点C的坐标,然后根据AC∥x轴可得点C、D的纵坐标相同,从而表示出点D的坐标,再代入反比例函数解析式进行计算即可得解.
解答 解:∵点B在反比例函数y=$\frac{k}{x}$的图象上,点B,C的横坐标都是3,
∴点B(3,$\frac{k}{3}$),
∵BC=2,
∴点C(3,$\frac{k}{3}$+2),
∵AC∥x轴,点D在AC上,且横坐标为1,
∴D(1,$\frac{k}{3}$+2),
∵点D也在反比例函数图象上,
∴$\frac{k}{3}$+2=k,
解得,k=3.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
9.下列选项中,可以用来说明命题“两个锐角的和是锐角”是假命题的反例的是( )
| A. | ∠A=30°,∠B=40° | B. | ∠A=30°,∠B=110° | C. | ∠A=30°,∠B=70° | D. | ∠A=30°,∠B=90° |
6.把抛物线y=x2-3向右平移2个单位,然后向上平移2个单位,则平移后得到的抛物线的解析式为( )
| A. | y=(x-2)2-1 | B. | y=(x+2)2-1 | C. | y=(x-2)2+1 | D. | y=(x+2)2+1 |
7. 我区为了解七年级学生的环保意识,在全区范围内组织七年级学生进行了一次环保知识测试,随机抽取了若干名学生的成绩(成绩为整数,满分100分),进行统计后,绘制出如下频数分布表和如图所示不完整的频数分布直方图.
我区为了解七年级学生的环保意识,在全区范围内组织七年级学生进行了一次环保知识测试,随机抽取了若干名学生的成绩(成绩为整数,满分100分),进行统计后,绘制出如下频数分布表和如图所示不完整的频数分布直方图.
请根据图表信息回答下列问题:
(1)在频数分布表中,a=60,b=0.05.并补全频数分别直方图.
(2)甲同学说:“我的成绩是此次抽样调查所得数据的中位数”,问甲同学的成绩应在什么范围?
(3)全区共有七年级学生5000名,若规定成绩在80分以上(不含80分)为优秀,估计这次考试中成绩为优秀的学生有多少人?
 我区为了解七年级学生的环保意识,在全区范围内组织七年级学生进行了一次环保知识测试,随机抽取了若干名学生的成绩(成绩为整数,满分100分),进行统计后,绘制出如下频数分布表和如图所示不完整的频数分布直方图.
我区为了解七年级学生的环保意识,在全区范围内组织七年级学生进行了一次环保知识测试,随机抽取了若干名学生的成绩(成绩为整数,满分100分),进行统计后,绘制出如下频数分布表和如图所示不完整的频数分布直方图.| 成绩 | 频数 | 频率 |
| 50.5~60.5 | 20 | 0.1 |
| 60.5~70.5 | 40 | 0.2 |
| 70.5~80.5 | 70 | 0.35 |
| 80.5~90.5 | a | 0.3 |
| 90.5~100.5 | 10 | b |
(1)在频数分布表中,a=60,b=0.05.并补全频数分别直方图.
(2)甲同学说:“我的成绩是此次抽样调查所得数据的中位数”,问甲同学的成绩应在什么范围?
(3)全区共有七年级学生5000名,若规定成绩在80分以上(不含80分)为优秀,估计这次考试中成绩为优秀的学生有多少人?
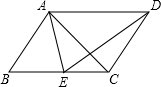 如图,在?ABCD中,E为BC边上一点,且AB=AE,若AE平分∠DAB,∠EAC=25°,则∠AED的度数是85度.
如图,在?ABCD中,E为BC边上一点,且AB=AE,若AE平分∠DAB,∠EAC=25°,则∠AED的度数是85度.