题目内容
19.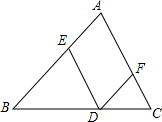 已知D为△ABC边BC上的一个动点(不与B,C重合),过D作DE∥AC交AB于点E,作DF∥AB交AC于点F.
已知D为△ABC边BC上的一个动点(不与B,C重合),过D作DE∥AC交AB于点E,作DF∥AB交AC于点F.(1)证明:△BDE∽△DCF;
(2)若△ABC的面积为10,点G为线段AF上的任意一点,设FC:AC=n,△DEG的面积为S,求S关于n的关系式,并求S的最大值.
分析 (1)根据相似三角形的判定证明即可;
(2)根据相似三角形的性质和二次函数的最值解答即可.
解答 解:(1)∵DF∥AB,
∴△DFC∽△BAC,
∵DE∥AC,
∴△BED∽△BAC
∴△DFC∽△BED;
(2)∵△BED∽△DFC∽△BAC,FC:AC=n,△ABC的面积为10,
∴${(\frac{CF}{CA})^2}=\frac{{{S_{△DFC}}}}{10}$,${S_{△DFC}}=10{n^2}$,${(\frac{BD}{BC})^2}=\frac{{{S_{△DEB}}}}{10}$,${S_{△DEB}}=10{(1-n)^2}$,${S_{AEDF}}=10-10{n^2}-10{(1-n)^2}$,
∵点G为线段AF上的任意一点,$S=\frac{1}{2}{S_{AEDF}}$,
∴S=-10n2+10n=-10$(n-\frac{1}{2})^{2}+2.5$,
∴S的最大值是2.5.
点评 此题考查相似三角形的综合题,关键是根据相似三角形的判定和性质进行解答.

练习册系列答案
相关题目
9.下列选项中,可以用来说明命题“两个锐角的和是锐角”是假命题的反例的是( )
| A. | ∠A=30°,∠B=40° | B. | ∠A=30°,∠B=110° | C. | ∠A=30°,∠B=70° | D. | ∠A=30°,∠B=90° |
7. 我区为了解七年级学生的环保意识,在全区范围内组织七年级学生进行了一次环保知识测试,随机抽取了若干名学生的成绩(成绩为整数,满分100分),进行统计后,绘制出如下频数分布表和如图所示不完整的频数分布直方图.
我区为了解七年级学生的环保意识,在全区范围内组织七年级学生进行了一次环保知识测试,随机抽取了若干名学生的成绩(成绩为整数,满分100分),进行统计后,绘制出如下频数分布表和如图所示不完整的频数分布直方图.
请根据图表信息回答下列问题:
(1)在频数分布表中,a=60,b=0.05.并补全频数分别直方图.
(2)甲同学说:“我的成绩是此次抽样调查所得数据的中位数”,问甲同学的成绩应在什么范围?
(3)全区共有七年级学生5000名,若规定成绩在80分以上(不含80分)为优秀,估计这次考试中成绩为优秀的学生有多少人?
 我区为了解七年级学生的环保意识,在全区范围内组织七年级学生进行了一次环保知识测试,随机抽取了若干名学生的成绩(成绩为整数,满分100分),进行统计后,绘制出如下频数分布表和如图所示不完整的频数分布直方图.
我区为了解七年级学生的环保意识,在全区范围内组织七年级学生进行了一次环保知识测试,随机抽取了若干名学生的成绩(成绩为整数,满分100分),进行统计后,绘制出如下频数分布表和如图所示不完整的频数分布直方图.| 成绩 | 频数 | 频率 |
| 50.5~60.5 | 20 | 0.1 |
| 60.5~70.5 | 40 | 0.2 |
| 70.5~80.5 | 70 | 0.35 |
| 80.5~90.5 | a | 0.3 |
| 90.5~100.5 | 10 | b |
(1)在频数分布表中,a=60,b=0.05.并补全频数分别直方图.
(2)甲同学说:“我的成绩是此次抽样调查所得数据的中位数”,问甲同学的成绩应在什么范围?
(3)全区共有七年级学生5000名,若规定成绩在80分以上(不含80分)为优秀,估计这次考试中成绩为优秀的学生有多少人?
14. 如图,在平面直角坐标系中,点A,B的坐标分别为(1,0),(0,2),某抛物线的顶点坐标为D(-1,1)且经过点B,连接AB,直线AB与此抛物线的另一个交点为C,则S△BCD:S△ABO=( )
如图,在平面直角坐标系中,点A,B的坐标分别为(1,0),(0,2),某抛物线的顶点坐标为D(-1,1)且经过点B,连接AB,直线AB与此抛物线的另一个交点为C,则S△BCD:S△ABO=( )
 如图,在平面直角坐标系中,点A,B的坐标分别为(1,0),(0,2),某抛物线的顶点坐标为D(-1,1)且经过点B,连接AB,直线AB与此抛物线的另一个交点为C,则S△BCD:S△ABO=( )
如图,在平面直角坐标系中,点A,B的坐标分别为(1,0),(0,2),某抛物线的顶点坐标为D(-1,1)且经过点B,连接AB,直线AB与此抛物线的另一个交点为C,则S△BCD:S△ABO=( )| A. | 8:1 | B. | 6:1 | C. | 5:1 | D. | 4:1 |
4.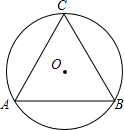 如图,等边△ABC是⊙O的内接三角形,则圆心O关于直线AB的对称点O′和⊙O的位置关系是( )
如图,等边△ABC是⊙O的内接三角形,则圆心O关于直线AB的对称点O′和⊙O的位置关系是( )
 如图,等边△ABC是⊙O的内接三角形,则圆心O关于直线AB的对称点O′和⊙O的位置关系是( )
如图,等边△ABC是⊙O的内接三角形,则圆心O关于直线AB的对称点O′和⊙O的位置关系是( )| A. | 在⊙O内 | B. | 在⊙O上 | C. | 在⊙O外 | D. | 不能确定 |
8.计算sin245°+tan60°•cos30°值为( )
| A. | 2 | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
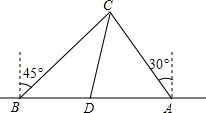 为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域.如图所示,AB=60($\sqrt{6}+\sqrt{2}$)海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120($\sqrt{6}-\sqrt{2}$)海里.
为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域.如图所示,AB=60($\sqrt{6}+\sqrt{2}$)海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120($\sqrt{6}-\sqrt{2}$)海里.