题目内容
14．在平面直角坐标系中，已知A（3，3），连接OA，过A作AB⊥x轴于B，P为线段OB上的一点，过P作x轴的垂线交OA于M，设OP=x，△POM的面积为S（1）试写出S与x之间的函数关系式；
（2）画出此函数的图象（在给定的平面直角坐标系中）
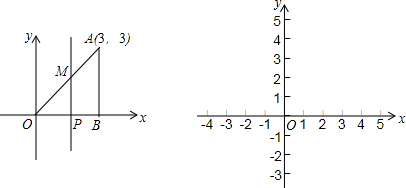
分析 （1）根据三角形的面积公式列出函数关系式即可；
（2）根据函数关系式画出函数图象即可．
解答 解：（1）∵A（3，3），
∴∠AOB=45°，
∴△OPM是等腰直角三角形，
∴S=$\frac{1}{2}$OP2=$\frac{1}{2}$x2（0≤x≤3）；
（2）函数的图象如图所示：
点评 本题主要考查了动点问题的函数图象，根据题意列出函数关系式是解决问题的关键．
练习册系列答案
名校提分一卷通系列答案
课程达标测试卷闯关100分系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
如图，依图填空：
2．
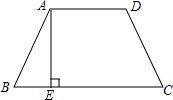如图所示，在梯形ABCD中，∠ABC=60°，AB=CD=AD，过点A作AE⊥BC于点E，AE=3，CE=3$\sqrt{3}$，则梯形ABCD的周长与面积分别是（ ）
如图所示，在梯形ABCD中，∠ABC=60°，AB=CD=AD，过点A作AE⊥BC于点E，AE=3，CE=3$\sqrt{3}$，则梯形ABCD的周长与面积分别是（ ）| A． | 8，9$\sqrt{3}$ | B． | 10$\sqrt{3}$，9$\sqrt{3}$ | C． | 9$\sqrt{3}$，10$\sqrt{3}$ | D． | 8$\sqrt{3}$，9$\sqrt{3}$ |
19．$-4{x^4}{y^2}{z^2}÷（-\frac{1}{2}{x^3}yz）$的结果是（ ）
| A． | 8xyz | B． | -8xyz | C． | 2xyz | D． | 8xy2z2 |
如图，已知抛物线y=x2过P（2，m），过P点的直线l与抛物线只有一个公共点，求直线l的解析式．
如图，在Rt△ABC和Rt△BAD中，∠C=∠D=90°，AD平分∠CAB，BC平分∠ABD，AD、BC相交于点O，求证：OC=OD．