题目内容
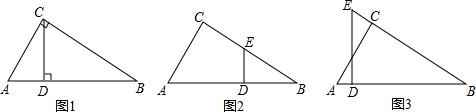
4. 如图,依图填空:
如图,依图填空:在△ABC中,BC边上的高是AB;
在△ABC中,AE边上的高是CD;
在△ABC中,EC边上的高是AB;
AB=CD=2,AE=3,则△AEC的面积S=3,CE=3.
分析 根据三角形的高线的定义和三角形的中线的性质解答.
解答 解:根据高的定义,在△ABC中,BC边上的高是AB;
在△ABC中,AE边上的高是CD;
在△ABC中,EC边上的高是AB;
AB=CD=2,AE=3,则△AEC的面积S=$\frac{1}{2}×2×3$=3,CE=$\frac{1}{2}×2×3÷2$=3.
故答案为:AB;CD;AB;3;3.
点评 本题主要考查了三角形的高的定义,熟记概念是解题的关键.

练习册系列答案
相关题目
14.下列变形,属于因式分解的有( )
①x2-16=(x+4)(x-4);②x2+3x-16=x(x+3)-16;③(x+4)(x-4)=x2-16;④${x^2}+1=x({x+\frac{1}{x}})$.
①x2-16=(x+4)(x-4);②x2+3x-16=x(x+3)-16;③(x+4)(x-4)=x2-16;④${x^2}+1=x({x+\frac{1}{x}})$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.若a(a-2b)+b2+2(a-b)+1=0,则a-b的值是( )
| A. | 1 | B. | -1 | C. | 0 | D. | 2 |