题目内容
8.等腰三角形的两边长分别为3和6,那么该三角形的周长为( )| A. | 12 | B. | 15 | C. | 10 | D. | 12或15 |
分析 求等腰三角形的周长,即是确定等腰三角形的腰与底的长求周长;题目给出等腰三角形有两条边长为3和6,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
解答 解:当等腰三角形的腰为3时,三边为3,3,6,3+3=6,三边关系不成立,
当等腰三角形的腰为6时,三边为3,6,6,三边关系成立,周长为3+6+6=15.
故选:B.
点评 本题考查了等腰三角形的性质和三角形的三边关系;题目从边的方面考查三角形,涉及分类讨论的思想方法.求三角形的周长,不能盲目地将三边长相加起来,而应养成检验三边长能否组成三角形的好习惯,把不符合题意的舍去.

练习册系列答案
相关题目
13.某商店在开业前,进了上衣、裤子与鞋子三种货物,其中裤子进了108条,三种货物进货数量的统计图如图甲所示.销售人员(销售上衣3人,销售裤子2人,销售鞋子1人)试销售了3天时间.经统计,这三天里三种货物每人每天销售数量统计图如图乙所示,三种货物3天的销售总量见表格(部分信息未给出).
(1)求所进上衣多少件?鞋子多少双?
(2)把表格补充完整.
(3)若销售人员不变,以同样的销售速度销售,请通过计算说明哪种货物最先售完?
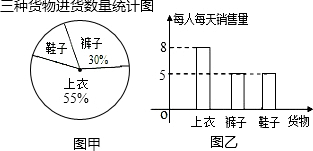
| 货物 | 上衣 (件) | 裤子 (条) | 鞋子 (双) |
| 3天的销售总量 | 72 | 30 | 15 |
(2)把表格补充完整.
(3)若销售人员不变,以同样的销售速度销售,请通过计算说明哪种货物最先售完?

3.已知点A(-1,y1),B(2,y2),C(3,y3)都在反比例函数y=-$\frac{5}{x}$的图象上,则下列结论中正确的是( )
| A. | y1<y2<y3 | B. | y2<y3<y1 | C. | y3<y2<y1 | D. | y1<y3<y2 |
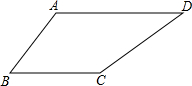 如图,四边形ABCD中,AB=BC=6cm,∠A=120°,∠B=60°,∠C=150°,求AD的长.
如图,四边形ABCD中,AB=BC=6cm,∠A=120°,∠B=60°,∠C=150°,求AD的长.