题目内容
8.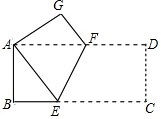 如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论:①AF=AE;②AF=EF;③△ABE≌△AGF;④EF=2$\sqrt{5}$,其中正确的个数有( )
如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论:①AF=AE;②AF=EF;③△ABE≌△AGF;④EF=2$\sqrt{5}$,其中正确的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 设BE=x,表示出CE=8-x,根据翻折的性质可得AE=CE,然后在Rt△ABE中,利用勾股定理列出方程求出x,再根据翻折的性质可得∠AEF=∠CEF,根据两直线平行,内错角相等可得∠AFE=∠CEF,然后求出∠AEF=∠AFE,根据等角对等边可得AE=AF,过点E作EH⊥AD于H,可得四边形ABEH是矩形,根据矩形的性质求出EH、AH,然后求出FH,再利用勾股定理列式计算即可得解.
解答 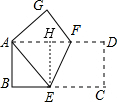 解:设BE=x,则CE=BC-BE=8-x,
解:设BE=x,则CE=BC-BE=8-x,
∵沿EF翻折后点C与点A重合,
∴AE=CE=8-x,
在Rt△ABE中,AB2+BE2=AE2,
即42+x2=(8-x)2
解得x=3,
∴AE=8-3=5,
由翻折的性质得,∠AEF=∠CEF,
∵矩形ABCD的对边AD∥BC,
∴∠AFE=∠CEF,
∴∠AEF=∠AFE,
∴AE=AF=5,
∴①正确;
∵△AEF不是等边三角形,
∴EF≠AF,
故②错误;
在Rt△ABE和Rt△AGF中,$\left\{\begin{array}{l}{AE=AF}\\{AG=AB}\end{array}\right.$,
∴△ABE≌△AGF(HL),
∴③正确;
过点E作EH⊥AD于H,则四边形ABEH是矩形,
∴EH=AB=4,
AH=BE=3,
∴FH=AF-AH=5-3=2,
在Rt△EFH中,EF=2$\sqrt{5}$,
∴④正确;
故选:C.
点评 本题考查了翻折变换的性质,矩形的判定与性质,勾股定理,熟记各性质并作利用勾股定理列方程求出BE的长度是解题的关键,也是本题的突破口.

练习册系列答案
相关题目
19.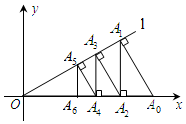 如图,过点A0(2,0)作直线l:y=$\frac{\sqrt{3}}{3}$x的垂线,垂足为点A1,过点A1作A1A2⊥x轴,垂足为点A2,过点A2作A2A3⊥l,垂足为点A3,…,这样依次下去,得到一组线段:A0A1,A1A2,A2A3,…,则线段A2016A2017的长为( )
如图,过点A0(2,0)作直线l:y=$\frac{\sqrt{3}}{3}$x的垂线,垂足为点A1,过点A1作A1A2⊥x轴,垂足为点A2,过点A2作A2A3⊥l,垂足为点A3,…,这样依次下去,得到一组线段:A0A1,A1A2,A2A3,…,则线段A2016A2017的长为( )
 如图,过点A0(2,0)作直线l:y=$\frac{\sqrt{3}}{3}$x的垂线,垂足为点A1,过点A1作A1A2⊥x轴,垂足为点A2,过点A2作A2A3⊥l,垂足为点A3,…,这样依次下去,得到一组线段:A0A1,A1A2,A2A3,…,则线段A2016A2017的长为( )
如图,过点A0(2,0)作直线l:y=$\frac{\sqrt{3}}{3}$x的垂线,垂足为点A1,过点A1作A1A2⊥x轴,垂足为点A2,过点A2作A2A3⊥l,垂足为点A3,…,这样依次下去,得到一组线段:A0A1,A1A2,A2A3,…,则线段A2016A2017的长为( )| A. | ($\frac{\sqrt{3}}{2}$)2015 | B. | ($\frac{\sqrt{3}}{2}$)2016 | C. | ($\frac{\sqrt{3}}{2}$)2017 | D. | ($\frac{\sqrt{3}}{2}$)2018 |
3. 如图,正方形ABCD的边长为4,点E、F分别在AB、BC上,且AE=BF=1,CE、DF交于点O,下列结论:①∠DOC=90°,②OC=OE,③CE=DF,④tan∠OCD=$\frac{4}{3}$,⑤S△DOC=S四边形EOFB中,正确的有( )
如图,正方形ABCD的边长为4,点E、F分别在AB、BC上,且AE=BF=1,CE、DF交于点O,下列结论:①∠DOC=90°,②OC=OE,③CE=DF,④tan∠OCD=$\frac{4}{3}$,⑤S△DOC=S四边形EOFB中,正确的有( )
 如图,正方形ABCD的边长为4,点E、F分别在AB、BC上,且AE=BF=1,CE、DF交于点O,下列结论:①∠DOC=90°,②OC=OE,③CE=DF,④tan∠OCD=$\frac{4}{3}$,⑤S△DOC=S四边形EOFB中,正确的有( )
如图,正方形ABCD的边长为4,点E、F分别在AB、BC上,且AE=BF=1,CE、DF交于点O,下列结论:①∠DOC=90°,②OC=OE,③CE=DF,④tan∠OCD=$\frac{4}{3}$,⑤S△DOC=S四边形EOFB中,正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.实数-$\sqrt{4}$,0,-π,$\sqrt{10}$,0.1010010001…(相邻两个1之间依次多一个0),$\frac{22}{7}$,其中无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.若函数y=(a+3)x+b-2的图象与x轴交于正半轴,与y轴交于负半轴,则( )
| A. | a>-3,b>2 | B. | a<-3,b<2 | C. | a>-3,b<2 | D. | a<-3,b>2 |
18.已知m是方程x2-2x-1=0的一个根,则代数式2m2-4m+2017的值为( )
| A. | 2019 | B. | 2018 | C. | 2016 | D. | 2015 |
 已知二次函数y=-x2+2x+m的部分图象如图,则关于x的一元二次方程-x2+2x+m=3的解为x=0或x=2.
已知二次函数y=-x2+2x+m的部分图象如图,则关于x的一元二次方程-x2+2x+m=3的解为x=0或x=2.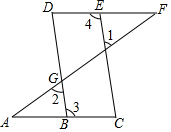 如图,点E在线段DF上,点B在线段AC上,若∠1=∠2,3=∠4,则∠A=∠F.请将下面证明过程或理由补充完整.
如图,点E在线段DF上,点B在线段AC上,若∠1=∠2,3=∠4,则∠A=∠F.请将下面证明过程或理由补充完整.