题目内容
3. 如图,正方形ABCD的边长为4,点E、F分别在AB、BC上,且AE=BF=1,CE、DF交于点O,下列结论:①∠DOC=90°,②OC=OE,③CE=DF,④tan∠OCD=$\frac{4}{3}$,⑤S△DOC=S四边形EOFB中,正确的有( )
如图,正方形ABCD的边长为4,点E、F分别在AB、BC上,且AE=BF=1,CE、DF交于点O,下列结论:①∠DOC=90°,②OC=OE,③CE=DF,④tan∠OCD=$\frac{4}{3}$,⑤S△DOC=S四边形EOFB中,正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由正方形ABCD的边长为4,AE=BF=1,利用SAS易证得△EBC≌△FCD,然后全等三角形的对应角相等,易证得①∠DOC=90°正确,③CE=DF正确;②由线段垂直平分线的性质与正方形的性质,可得②错误;易证得∠OCD=∠DFC,即可求得④正确;由①易证得⑤正确.
解答 解:∵正方形ABCD的边长为4,
∴BC=CD=4,∠B=∠DCF=90°,
∵AE=BF=1,
∴BE=CF=4-1=3,
在△EBC和△FCD中,
$\left\{\begin{array}{l}{BC=CD}\\{∠B=∠DCF}\\{BE=CF}\end{array}\right.$,
∴△EBC≌△FCD(SAS),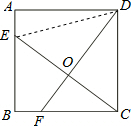
∴∠CFD=∠BEC,CE=DF,故③正确,
∴∠BCE+∠BEC=∠BCE+∠CFD=90°,
∴∠DOC=90°;故①正确;
连接DE,如图所示:
若OC=OE,
∵DF⊥EC,
∴CD=DE,
∵CD=AD<DE(矛盾),故②错误;
∵∠OCD+∠CDF=90°,∠CDF+∠DFC=90°,
∴∠OCD=∠DFC,
∴tan∠OCD=tan∠DFC=$\frac{DC}{FC}$=$\frac{4}{3}$,故④正确;
∵△EBC≌△FCD,
∴S△EBC=S△FCD,
∴S△EBC-S△FOC=S△FCD-S△FOC,
即S△ODC=S四边形BEOF.故⑤正确;
故正确的有:①③④⑤,
故选D.
点评 此题考查了正方形的性质、全等三角形的判定与性质、直角三角形的性质以及三角函数等知识.此题综合性较强,难度适中,注意掌握数形结合思想与转化思想的应用.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
18.比-1小2017的数是( )
| A. | -2016 | B. | 2016 | C. | 2018 | D. | -2018 |
8.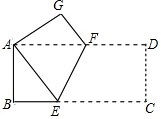 如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论:①AF=AE;②AF=EF;③△ABE≌△AGF;④EF=2$\sqrt{5}$,其中正确的个数有( )
如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论:①AF=AE;②AF=EF;③△ABE≌△AGF;④EF=2$\sqrt{5}$,其中正确的个数有( )
 如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论:①AF=AE;②AF=EF;③△ABE≌△AGF;④EF=2$\sqrt{5}$,其中正确的个数有( )
如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论:①AF=AE;②AF=EF;③△ABE≌△AGF;④EF=2$\sqrt{5}$,其中正确的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.已知点A与点B(-4,-5)关于x轴对称,则A点坐标是( )
| A. | (4,-5) | B. | (4,5) | C. | (-4,-5) | D. | (-4,5) |
 如图,在矩形ABCD中,对角线AC、BD交于点O,若∠AOD=120°,AB=1,则△OAB的周长为3.
如图,在矩形ABCD中,对角线AC、BD交于点O,若∠AOD=120°,AB=1,则△OAB的周长为3. 如图,抛物线y=ax2+3x交x轴正半轴于点A(6,0),顶点为M,对称轴MB交x轴于点B,过点C(2,0)作射线CD交MB于点D(D在x轴上方),OE∥CD交MB于点E,EF∥x轴交CD于点F,作直线MF.
如图,抛物线y=ax2+3x交x轴正半轴于点A(6,0),顶点为M,对称轴MB交x轴于点B,过点C(2,0)作射线CD交MB于点D(D在x轴上方),OE∥CD交MB于点E,EF∥x轴交CD于点F,作直线MF.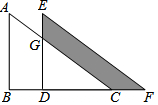 在直角三角形ABC中,AB=8,将直角三角形ABC沿BC所在直线向右平移6个单位可以得到直角三角形DEF,此时,EG=3,则图中阴影部分的面积是39.
在直角三角形ABC中,AB=8,将直角三角形ABC沿BC所在直线向右平移6个单位可以得到直角三角形DEF,此时,EG=3,则图中阴影部分的面积是39.