题目内容
19.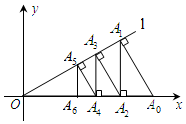 如图,过点A0(2,0)作直线l:y=$\frac{\sqrt{3}}{3}$x的垂线,垂足为点A1,过点A1作A1A2⊥x轴,垂足为点A2,过点A2作A2A3⊥l,垂足为点A3,…,这样依次下去,得到一组线段:A0A1,A1A2,A2A3,…,则线段A2016A2017的长为( )
如图,过点A0(2,0)作直线l:y=$\frac{\sqrt{3}}{3}$x的垂线,垂足为点A1,过点A1作A1A2⊥x轴,垂足为点A2,过点A2作A2A3⊥l,垂足为点A3,…,这样依次下去,得到一组线段:A0A1,A1A2,A2A3,…,则线段A2016A2017的长为( )| A. | ($\frac{\sqrt{3}}{2}$)2015 | B. | ($\frac{\sqrt{3}}{2}$)2016 | C. | ($\frac{\sqrt{3}}{2}$)2017 | D. | ($\frac{\sqrt{3}}{2}$)2018 |
分析 根据含30°的直角三角形的性质结合图形即可得到规律“OAn=($\frac{\sqrt{3}}{2}$)nOA=2($\frac{\sqrt{3}}{2}$)n,依此规律即可解决问题.
解答 解:由y=$\frac{\sqrt{3}}{3}$x,得
l的倾斜角为30°,
点A0坐标为(2,0),
∴OA0=2,
∴OA1=$\frac{\sqrt{3}}{2}$OA0=$\sqrt{3}$,OA2=$\frac{\sqrt{3}}{2}$OA1═$\frac{3}{2}$,OA3=$\frac{\sqrt{3}}{2}$OA2═$\frac{3\sqrt{3}}{4}$,OA4=$\frac{\sqrt{3}}{2}$OA3═$\frac{9}{8}$,…,
∴OAn=($\frac{\sqrt{3}}{2}$)nOA=2($\frac{\sqrt{3}}{2}$)n.
∴OA2016=2×($\frac{\sqrt{3}}{2}$)2016,
A2016A2107的长$\frac{1}{2}$×2×($\frac{\sqrt{3}}{2}$)2016=($\frac{\sqrt{3}}{2}$)2016,
故选:B.
点评 本题考查了规律型中点的坐标以及含30度角的直角三角形,利用“在直角三角形中,30°角所对的直角边等于斜边的一半”结合图形找出变化规律OAn=($\frac{\sqrt{3}}{2}$)nOA=2($\frac{\sqrt{3}}{2}$)n是解题的关键.

练习册系列答案
相关题目
10.平行四边形的一边长为 10cm,那么这个平行四边形的两条对角线长可以是( )
| A. | 4cm 和 6cm | B. | 6cm 和 8cm | C. | 20cm 和 30cm | D. | 8cm 和 12cm |
8.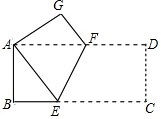 如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论:①AF=AE;②AF=EF;③△ABE≌△AGF;④EF=2$\sqrt{5}$,其中正确的个数有( )
如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论:①AF=AE;②AF=EF;③△ABE≌△AGF;④EF=2$\sqrt{5}$,其中正确的个数有( )
 如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论:①AF=AE;②AF=EF;③△ABE≌△AGF;④EF=2$\sqrt{5}$,其中正确的个数有( )
如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论:①AF=AE;②AF=EF;③△ABE≌△AGF;④EF=2$\sqrt{5}$,其中正确的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.下列方程中,属于二元一次方程的是( )
| A. | y+z=3 | B. | x+y-z=6 | C. | 2xz-y=1 | D. | x2+y=6 |
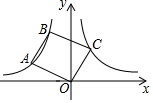 如图,点A、B在双曲线y=$\frac{3}{x}$(x<0)上,连接OA、AB,以OA、AB为边作?OABC.若点C恰落在双曲线y=$\frac{2}{x}$(x>0)上,此时?OABC的面积为2$\sqrt{7}$.
如图,点A、B在双曲线y=$\frac{3}{x}$(x<0)上,连接OA、AB,以OA、AB为边作?OABC.若点C恰落在双曲线y=$\frac{2}{x}$(x>0)上,此时?OABC的面积为2$\sqrt{7}$. 如图,抛物线y=ax2+3x交x轴正半轴于点A(6,0),顶点为M,对称轴MB交x轴于点B,过点C(2,0)作射线CD交MB于点D(D在x轴上方),OE∥CD交MB于点E,EF∥x轴交CD于点F,作直线MF.
如图,抛物线y=ax2+3x交x轴正半轴于点A(6,0),顶点为M,对称轴MB交x轴于点B,过点C(2,0)作射线CD交MB于点D(D在x轴上方),OE∥CD交MB于点E,EF∥x轴交CD于点F,作直线MF.