题目内容
20.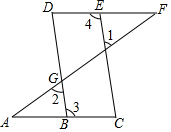 如图,点E在线段DF上,点B在线段AC上,若∠1=∠2,3=∠4,则∠A=∠F.请将下面证明过程或理由补充完整.
如图,点E在线段DF上,点B在线段AC上,若∠1=∠2,3=∠4,则∠A=∠F.请将下面证明过程或理由补充完整.证明∵∠1=∠2(已知),∠2=∠DGF(对顶角相等),
∴∠1=∠DGF,
∴BD∥CE(同位角相等,两直线平行),
∴∠3+∠C=180°(两直线平行,同旁内角互补);
又∵∠3=∠4(已知),
∴∠4+∠C=180°,
∴DF∥AC(同旁内角互补,两直线平行),
∴∠A=∠F(两直线平行,内错角相等).
分析 求出∠1=∠DGF,根据平行线的判定得出BD∥CE,根据平行线的性质得出∠3+∠C=180°,求出∠4+∠C=180°,根据平行线的判定得出DF∥AC即可.
解答 证明∵∠1=∠2(已知),∠2=∠DGF(对顶角相等),
∴∠1=∠DGF,
∴BD∥CE(同位角相等,两直线平行),
∴∠3+∠C=180°(两直线平行,同旁内角互补);
又∵∠3=∠4(已知),
∴∠4+∠C=180°,
∴DF∥AC(同旁内角互补,两直线平行),
∴∠A=∠F(两直线平行,内错角相等),
故答案为:对顶角相等,同位角相等,两直线平行,两直线平行,同旁内角互补,DF,AC,两直线平行,内错角相等.
点评 本题考查了平行线的性质和判定,能灵活运用平行线的性质和判定定理进行推理是解此题的关键.

练习册系列答案
相关题目
10.平行四边形的一边长为 10cm,那么这个平行四边形的两条对角线长可以是( )
| A. | 4cm 和 6cm | B. | 6cm 和 8cm | C. | 20cm 和 30cm | D. | 8cm 和 12cm |
8.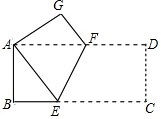 如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论:①AF=AE;②AF=EF;③△ABE≌△AGF;④EF=2$\sqrt{5}$,其中正确的个数有( )
如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论:①AF=AE;②AF=EF;③△ABE≌△AGF;④EF=2$\sqrt{5}$,其中正确的个数有( )
 如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论:①AF=AE;②AF=EF;③△ABE≌△AGF;④EF=2$\sqrt{5}$,其中正确的个数有( )
如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论:①AF=AE;②AF=EF;③△ABE≌△AGF;④EF=2$\sqrt{5}$,其中正确的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.已知点A与点B(-4,-5)关于x轴对称,则A点坐标是( )
| A. | (4,-5) | B. | (4,5) | C. | (-4,-5) | D. | (-4,5) |
9.下列方程中,属于二元一次方程的是( )
| A. | y+z=3 | B. | x+y-z=6 | C. | 2xz-y=1 | D. | x2+y=6 |
10.已知∠A与∠B互为余角,∠C与∠B互为补角,则∠C比∠A大( )
| A. | 45° | B. | 90° | C. | 135° | D. | D180° |
 如图,抛物线y=ax2+3x交x轴正半轴于点A(6,0),顶点为M,对称轴MB交x轴于点B,过点C(2,0)作射线CD交MB于点D(D在x轴上方),OE∥CD交MB于点E,EF∥x轴交CD于点F,作直线MF.
如图,抛物线y=ax2+3x交x轴正半轴于点A(6,0),顶点为M,对称轴MB交x轴于点B,过点C(2,0)作射线CD交MB于点D(D在x轴上方),OE∥CD交MB于点E,EF∥x轴交CD于点F,作直线MF.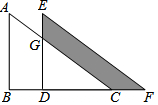 在直角三角形ABC中,AB=8,将直角三角形ABC沿BC所在直线向右平移6个单位可以得到直角三角形DEF,此时,EG=3,则图中阴影部分的面积是39.
在直角三角形ABC中,AB=8,将直角三角形ABC沿BC所在直线向右平移6个单位可以得到直角三角形DEF,此时,EG=3,则图中阴影部分的面积是39.