题目内容
12.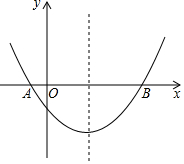 如图,抛物线经过A(-1,0),B(5,0),C(0,-$\frac{5}{2}$)三点.
如图,抛物线经过A(-1,0),B(5,0),C(0,-$\frac{5}{2}$)三点.(1)求抛物线的解析式;
(2)在直线BC下方的抛物线上有一动点P,使△PBC得面积最大,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,直接写出点N的坐标;若不存在,请说明理由.
分析 (1)设抛物线的解析式为y=ax2+bx+c(a≠0),再把A(-1,0),B(5,0),C(0,-$\frac{5}{2}$)三点代入求出a、b、c的值即可;
(2)根据平行于y轴直线上两点间的距离是较大的纵坐标减较的纵坐标,可得PD的长,根据三角形的面积公式,可得二次函数,根据二次函数的性质,可得答案;
(3)分点N在x轴下方或上方两种情况进行讨论.
解答 解:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),
∵A(-1,0),B(5,0),C(0,-$\frac{5}{2}$)三点在抛物线上,
∴$\left\{\begin{array}{l}{a-b+c=0}\\{25a+5b+c=0}\\{c=-\frac{5}{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-2}\\{c=-\frac{5}{2}}\end{array}\right.$.
∴抛物线的解析式为:y=$\frac{1}{2}$x2-2x-$\frac{5}{2}$;
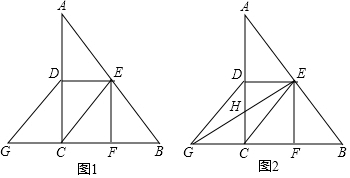
(2)如图1 ,
,
作PE⊥AB于E交BC于D点,
BC的解析式为y=$\frac{1}{2}$x-$\frac{5}{2}$,
设P点坐标(m,$\frac{1}{2}$m2-2m-$\frac{5}{2}$),D(m,$\frac{1}{2}$m-$\frac{5}{2}$),
PD的长为$\frac{1}{2}$m-$\frac{5}{2}$-($\frac{1}{2}$m2-2m-$\frac{5}{2}$)=-$\frac{1}{2}$m2+$\frac{5}{2}$m,
S△PBC=$\frac{1}{2}$PD•xB=$\frac{1}{2}$×(-$\frac{1}{2}$m2+$\frac{5}{2}$m)×5=-$\frac{5}{4}$m2+$\frac{25}{4}$m=-$\frac{5}{4}$(m-$\frac{5}{2}$)2+$\frac{125}{16}$,
当m=$\frac{5}{2}$时,S最大,
$\frac{1}{2}$m2-2m-$\frac{5}{2}$=-$\frac{35}{8}$,
即P点坐标为($\frac{5}{2}$,-$\frac{35}{8}$).
(3)存在.
如图2所示 ,
,
①当点N在x轴下方时,
∵抛物线的对称轴为直线x=2,C(0,-$\frac{5}{2}$),
∴N1(4,-$\frac{5}{2}$);
②当点N在x轴上方时,
如图,过点N2作N2D⊥x轴于点D,
在△AN2D与△M2CO中,
$\left\{\begin{array}{l}{∠{N}_{2}AD=∠C{M}_{2}O}\\{A{N}_{2}=C{M}_{2}}\\{∠A{N}_{2}D=∠{M}_{2}CO}\end{array}\right.$
∴△AN2D≌△M2CO(ASA),
∴N2D=OC=$\frac{5}{2}$,即N2点的纵坐标为$\frac{5}{2}$.
∴$\frac{1}{2}$x2-2x-$\frac{5}{2}$=$\frac{5}{2}$,
解得x=2+$\sqrt{14}$或x=2-$\sqrt{14}$,
∴N2(2+$\sqrt{14}$,$\frac{5}{2}$),N3(2-$\sqrt{14}$,$\frac{5}{2}$).
综上所述,符合条件的点N的坐标为(4,-$\frac{5}{2}$),(2+$\sqrt{14}$,$\frac{5}{2}$)或(2-$\sqrt{14}$,$\frac{5}{2}$).
点评 本题考查的是二次函数综合题,涉及到用待定系数法求一次函数与二次函数的解析式、平行四边的判定与性质、全等三角形等知识,解(2)的关键是平行于y轴直线上两点间的距离是较大的纵坐标减较的纵坐标得出PD的长,在解答(3)时要注意进行分类讨论.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案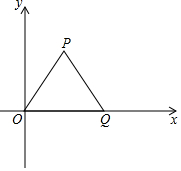 如图△OPQ是边长为$\sqrt{2}$的等边三角形,若反比例函数y=$\frac{k}{x}$的图象过点P.
如图△OPQ是边长为$\sqrt{2}$的等边三角形,若反比例函数y=$\frac{k}{x}$的图象过点P.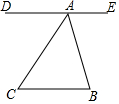 如图所示,已知DE∥BC,AC平分∠BAD,∠B=80°,求∠C的大小.
如图所示,已知DE∥BC,AC平分∠BAD,∠B=80°,求∠C的大小.
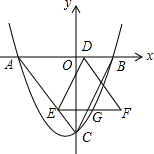 如图,抛物线y=ax2+bx-4经过A(-3,0),B(2,0)两点,与y轴的交点为C,连接AC、BC,D为线段AB上的动点,DE∥BC交AC于E,A关于DE的对称点为F,连接DF、EF.
如图,抛物线y=ax2+bx-4经过A(-3,0),B(2,0)两点,与y轴的交点为C,连接AC、BC,D为线段AB上的动点,DE∥BC交AC于E,A关于DE的对称点为F,连接DF、EF.