题目内容
1.在△ABC中,∠C=90°,D是AC的中点,E是AB的中点,作EF⊥BC于F,延长BC至G,使CG=BF,连接CE、DE、DG.(1)如图1,求证:四边形CEDG是平行四边形;
(2)如图2,连接EG交AC于点H,若EG⊥AB,请直接写出图2中所有长度等于$\sqrt{2}$GH的线段.
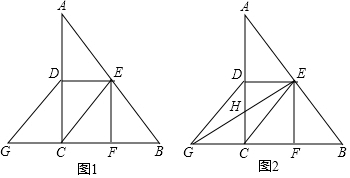
分析 (1)欲证明四边形CEDG是平行四边形,只要证明DE∥CG,DE=CG即可.
(2)由四边形四边形CEDG是平行四边形,推出DH=CH,GH=HE,设DH=CH=a,则AD=CD=2a,由∠A=∠A,∠AEH=∠ADE=90°,推出△ADE∽△AEH,推出AE2=AD•AH=2a•3a=6a2,推出AE=$\sqrt{6}$a,在Rt△AEH中,HE=$\sqrt{A{H}^{2}-A{E}^{2}}$=$\sqrt{(3a)^{2}-(\sqrt{6}a)^{2}}$=$\sqrt{3}$a,推出AE=$\sqrt{2}$HE,因为GH=HE,AE=EB=CE=CD,即可推出线段AE、EB、EC、GD都是线段GH的$\sqrt{2}$倍.
解答 (1)证明:如图1中,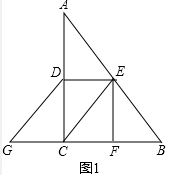
∵∠ACB=90°,AE=EB,
∴EC=EA=EB,
∵EF⊥BC,
∴CF=FB,
∵AD=DC,AE=EB,
∴DE∥BC,DE=$\frac{1}{2}$BC=BF,
∵CG=BF,
∴DE=CG,DE∥CG,
∴四边形四边形CEDG是平行四边形;
(2)解:如图2中,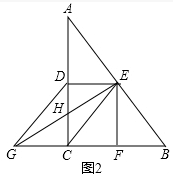
∵四边形四边形CEDG是平行四边形,
∴DH=CH,GH=HE,设DH=CH=a,则AD=CD=2a,
∵∠A=∠A,∠AEH=∠ADE=90°,
∴△ADE∽△AEH,
∴AE2=AD•AH=2a•3a=6a2,
∴AE=$\sqrt{6}$a,
在Rt△AEH中,HE=$\sqrt{A{H}^{2}-A{E}^{2}}$=$\sqrt{(3a)^{2}-(\sqrt{6}a)^{2}}$=$\sqrt{3}$a,
∴AE=$\sqrt{2}$HE,
∵GH=HE,AE=EB=CE=CD,
∴线段AE、EB、EC、GD都是线段GH的$\sqrt{2}$倍.
点评 本题考查平行四边形的性质、三角形的中位线定理、勾股定理、相似三角形的判定和性质等知识,解题的关键是学会利用参数解决问题,属于中考常考题型.

 阅读快车系列答案
阅读快车系列答案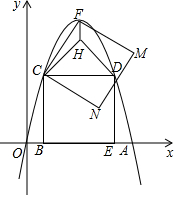 如图,在平面直角坐标系中,抛物线y=ax2-6ax(a<0)与x轴正半轴交于点A,矩形BCDE的顶点B、E均在x轴上,C、D均在抛物线上,且点B的坐标为(1,0),抛物线的顶点为F,以CF为边作正方形CFMN,以CD为底边向上作等腰直角三角形CDH,连结FH.
如图,在平面直角坐标系中,抛物线y=ax2-6ax(a<0)与x轴正半轴交于点A,矩形BCDE的顶点B、E均在x轴上,C、D均在抛物线上,且点B的坐标为(1,0),抛物线的顶点为F,以CF为边作正方形CFMN,以CD为底边向上作等腰直角三角形CDH,连结FH.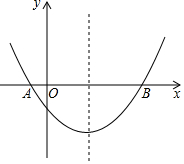 如图,抛物线经过A(-1,0),B(5,0),C(0,-$\frac{5}{2}$)三点.
如图,抛物线经过A(-1,0),B(5,0),C(0,-$\frac{5}{2}$)三点. 如图,三角形ABC中,∠B=90°,D在AC边上,DF⊥BC于F,DE⊥AB于E,说明:AE∥DF,BC∥DE.
如图,三角形ABC中,∠B=90°,D在AC边上,DF⊥BC于F,DE⊥AB于E,说明:AE∥DF,BC∥DE.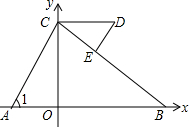 如图,平面直角坐标系中,已知C(0,5),D(a,5)(a>0),A,B在x轴上,若∠1=∠D,请写出∠ACB和∠BED数量关系并证明你的结论.
如图,平面直角坐标系中,已知C(0,5),D(a,5)(a>0),A,B在x轴上,若∠1=∠D,请写出∠ACB和∠BED数量关系并证明你的结论.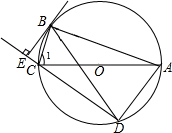 如图,⊙O是△ABC的外接圆,AC为直径,$\widehat{BD}$=$\widehat{BA}$,BE⊥DC交DC的延长线于点E.
如图,⊙O是△ABC的外接圆,AC为直径,$\widehat{BD}$=$\widehat{BA}$,BE⊥DC交DC的延长线于点E.