题目内容
3.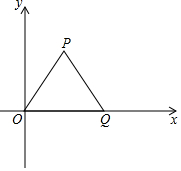 如图△OPQ是边长为$\sqrt{2}$的等边三角形,若反比例函数y=$\frac{k}{x}$的图象过点P.
如图△OPQ是边长为$\sqrt{2}$的等边三角形,若反比例函数y=$\frac{k}{x}$的图象过点P.(Ⅰ)求点P的坐标和k的值;
(Ⅱ)若在这个反比例函数的图象上有两个点(x1,y1)(x2,y2),且x1<x2<0,请比较y1与y2的大小.
分析 (Ⅰ)根据等边三角形的性质得到点P的坐标,根据待定系数法可求k的值;
(Ⅱ)由k的值大于0,得到在每一个象限,y随x的增大而减小,利用增减性即可判断.
解答 解:(1)∵△OPQ是边长为$\sqrt{2}$的等边三角形,
∴点P的坐标为($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{6}}{2}$)
∵反比例函数的图象过点P,
∴$\frac{\sqrt{6}}{2}$=$\frac{k}{\frac{\sqrt{2}}{2}}$,
解得k=$\frac{\sqrt{3}}{2}$.
(2)∵k=$\frac{\sqrt{3}}{2}$>0,
在这个反比例函数的图象上有两个点(x1,y1)(x2,y2),且x1<x2<0,
∴y1>y2.
点评 此题考查了待定系数法确定反比例函数解析式,以及反比例函数的图象与性质,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
 如图,正方形网格中每个小正方形边长都是1,每个小格的顶点叫格点,以格点为顶点的三角形叫做格点三角形.
如图,正方形网格中每个小正方形边长都是1,每个小格的顶点叫格点,以格点为顶点的三角形叫做格点三角形.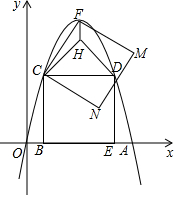 如图,在平面直角坐标系中,抛物线y=ax2-6ax(a<0)与x轴正半轴交于点A,矩形BCDE的顶点B、E均在x轴上,C、D均在抛物线上,且点B的坐标为(1,0),抛物线的顶点为F,以CF为边作正方形CFMN,以CD为底边向上作等腰直角三角形CDH,连结FH.
如图,在平面直角坐标系中,抛物线y=ax2-6ax(a<0)与x轴正半轴交于点A,矩形BCDE的顶点B、E均在x轴上,C、D均在抛物线上,且点B的坐标为(1,0),抛物线的顶点为F,以CF为边作正方形CFMN,以CD为底边向上作等腰直角三角形CDH,连结FH. 平行四边形ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
平行四边形ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.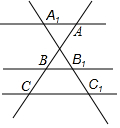 如图,直线AlA∥BB1∥CC1,若AB=8,BC=4,A1B1=6,则线段A1C1的长是9.
如图,直线AlA∥BB1∥CC1,若AB=8,BC=4,A1B1=6,则线段A1C1的长是9.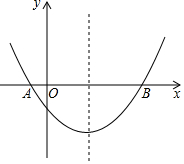 如图,抛物线经过A(-1,0),B(5,0),C(0,-$\frac{5}{2}$)三点.
如图,抛物线经过A(-1,0),B(5,0),C(0,-$\frac{5}{2}$)三点.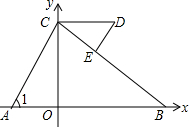 如图,平面直角坐标系中,已知C(0,5),D(a,5)(a>0),A,B在x轴上,若∠1=∠D,请写出∠ACB和∠BED数量关系并证明你的结论.
如图,平面直角坐标系中,已知C(0,5),D(a,5)(a>0),A,B在x轴上,若∠1=∠D,请写出∠ACB和∠BED数量关系并证明你的结论.