题目内容
20.先化简,再求代数式$\frac{{a}^{2}+3a}{{a}^{2}+4a+4}$÷$\frac{a+3}{a+2}$-$\frac{2}{a+2}$的值,其中a=2cos45°-2.分析 先根据分式的混合运算顺序和法则化简原式,再将计算出来的a的知道代入求解可得.
解答 解:原式=$\frac{a(a+3)}{(a+2)^{2}}$•$\frac{a+2}{a+3}$-$\frac{2}{a+2}$
=$\frac{a}{a+2}$-$\frac{2}{a+2}$
=$\frac{a-2}{a+2}$,
当a=2cos45°-2=2×$\frac{\sqrt{2}}{2}$-2=$\sqrt{2}$-2时,
原式=$\frac{\sqrt{2}-2-2}{\sqrt{2}-2+2}$=$\frac{\sqrt{2}-4}{\sqrt{2}}$=1-2$\sqrt{2}$.
点评 本题主要考查分式的化简求值和特殊锐角的三角函数值,熟练掌握分式的混合运算顺序和法则是解题的关键.

练习册系列答案
相关题目
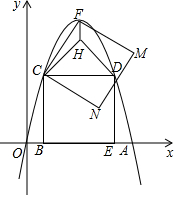 如图,在平面直角坐标系中,抛物线y=ax2-6ax(a<0)与x轴正半轴交于点A,矩形BCDE的顶点B、E均在x轴上,C、D均在抛物线上,且点B的坐标为(1,0),抛物线的顶点为F,以CF为边作正方形CFMN,以CD为底边向上作等腰直角三角形CDH,连结FH.
如图,在平面直角坐标系中,抛物线y=ax2-6ax(a<0)与x轴正半轴交于点A,矩形BCDE的顶点B、E均在x轴上,C、D均在抛物线上,且点B的坐标为(1,0),抛物线的顶点为F,以CF为边作正方形CFMN,以CD为底边向上作等腰直角三角形CDH,连结FH. 平行四边形ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
平行四边形ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.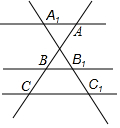 如图,直线AlA∥BB1∥CC1,若AB=8,BC=4,A1B1=6,则线段A1C1的长是9.
如图,直线AlA∥BB1∥CC1,若AB=8,BC=4,A1B1=6,则线段A1C1的长是9.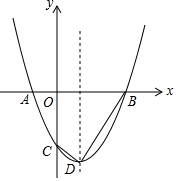 如图,O是坐标原点,过点A(-1,0)的抛物线y=x2-bx-3与x轴的另一个交点为B,与y轴交于点C,其顶点为D点
如图,O是坐标原点,过点A(-1,0)的抛物线y=x2-bx-3与x轴的另一个交点为B,与y轴交于点C,其顶点为D点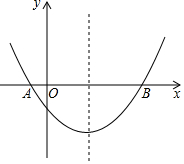 如图,抛物线经过A(-1,0),B(5,0),C(0,-$\frac{5}{2}$)三点.
如图,抛物线经过A(-1,0),B(5,0),C(0,-$\frac{5}{2}$)三点. 如图,三角形ABC中,∠B=90°,D在AC边上,DF⊥BC于F,DE⊥AB于E,说明:AE∥DF,BC∥DE.
如图,三角形ABC中,∠B=90°,D在AC边上,DF⊥BC于F,DE⊥AB于E,说明:AE∥DF,BC∥DE.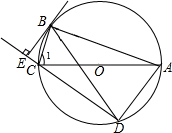 如图,⊙O是△ABC的外接圆,AC为直径,$\widehat{BD}$=$\widehat{BA}$,BE⊥DC交DC的延长线于点E.
如图,⊙O是△ABC的外接圆,AC为直径,$\widehat{BD}$=$\widehat{BA}$,BE⊥DC交DC的延长线于点E.