题目内容
11. 如图,抛物线y=x2-3x+$\frac{5}{4}$与x轴相交A、B两点,与y轴相交于点C,D是直线BC下方的抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E.
如图,抛物线y=x2-3x+$\frac{5}{4}$与x轴相交A、B两点,与y轴相交于点C,D是直线BC下方的抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E.(1)求直线BC对应的函数解析式;
(2)当线段DE的长度最长时,求点D的坐标.
分析 (1)求出B、C两点坐标,利用待定系数法即可解决问题.
(2)设D坐标为(m,m2-3m+$\frac{5}{4}$),则点E坐标为(m,-$\frac{1}{2}$m+$\frac{5}{4}$),设DE的长为d,构建二次函数,利用二次函数的性质即可解决问题.
解答 解:(1)对于抛物线y=x2-3x+$\frac{5}{4}$,令y=0,得x2-3x+$\frac{5}{4}$=0,解得x=$\frac{1}{2}$或$\frac{5}{2}$,
∴A($\frac{1}{2}$,0),B($\frac{5}{2}$,0),
令x=0,得y=$\frac{5}{4}$,
∴C(0,$\frac{5}{4}$).
设直线BC的解析式为y=kx+b,
则有$\left\{\begin{array}{l}{\frac{5}{2}k+b=0}\\{b=\frac{5}{4}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=\frac{5}{4}}\end{array}\right.$,
∴直线BC的解析式为y=-$\frac{1}{2}$x+$\frac{5}{4}$.
(2)设D坐标为(m,m2-3m+$\frac{5}{4}$),
∴点E坐标为(m,-$\frac{1}{2}$m+$\frac{5}{4}$),设DE的长为d,
∵D是直线BC下方的一点,
∴d=(-$\frac{1}{2}$m+$\frac{5}{4}$)-(m2-3m+$\frac{5}{4}$)=-m2+$\frac{5}{2}$m=-(m-$\frac{5}{4}$)2+$\frac{25}{16}$,
∴当m=$\frac{5}{4}$时,线段DE的长度最长,此时D($\frac{5}{4}$,-$\frac{15}{16}$).
点评 本题考查抛物线与x轴的交点、一次函数的应用、待定系数法等知识,解题的关键是熟练掌握待定系数法确定函数解析式,学会构建二次函数解决最值问题,属于中考常考题型.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案| A. | 若y是x的函数,那么x也是y的函数 | |
| B. | 两个变量之间的函数关系一定能用数学式子表达 | |
| C. | 若y是x的函数,则当y取一个值时,一定有唯一的x值与它对应 | |
| D. | 一个人的身高也可以看作他年龄的函数 |
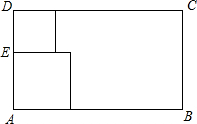 如图所示,从一张矩形纸较短的边上找一点E.过点E剪下两个正方形,它们的边长分别是AE,DE,要使剪下的两个正方形的面积和最小,点E应选在何处?
如图所示,从一张矩形纸较短的边上找一点E.过点E剪下两个正方形,它们的边长分别是AE,DE,要使剪下的两个正方形的面积和最小,点E应选在何处? 如图,已知P是两直角边分别为3cm、4cm的Rt△ABC斜边AB上的任意一点,以CP为直径作圆,则该圆的面积y(cm2)与CP的长x(cm)之间的函数关系式是y=$\frac{1}{4}$πx2,自变量x的取值范围是2.4≤x≤4,y的最小值是1.44π,y的最大值是4π.
如图,已知P是两直角边分别为3cm、4cm的Rt△ABC斜边AB上的任意一点,以CP为直径作圆,则该圆的面积y(cm2)与CP的长x(cm)之间的函数关系式是y=$\frac{1}{4}$πx2,自变量x的取值范围是2.4≤x≤4,y的最小值是1.44π,y的最大值是4π. 已知C、D是线段AB上的两点,点C是AD的中点,AB=10cm,AC=4cm,则DB的长度为2 cm.
已知C、D是线段AB上的两点,点C是AD的中点,AB=10cm,AC=4cm,则DB的长度为2 cm.