题目内容
5.抛物线y=ax2+bx+c满足下列条件:(1)4a-b=0; (2)a-b+c>0;(3)与x轴有两个交点,且两交点的距离小于2.以下有四个结论:①a<0;②c>0;③ac=$\frac{1}{4}$b2;④$\frac{c}{4}$<a<$\frac{c}{3}$.则其中正确结论的序号是②④.分析 先确定抛物线的对称轴为直线x=-$\frac{b}{2a}$=-2,由于抛物线与x轴有两个交点,且两交点的距离小于2,x=-1时,a-b+c>0,则可判断抛物线与x轴的一个交点在(-1,0)和(0,0)之间,所以抛物线的开口向上,抛物线与y轴的交点在x轴上方,则可对①②进行判断;利用两交点的距离小于2得到$\frac{\sqrt{{b}^{2}-4ac}}{a}$<2,则可得到a<$\frac{c}{3}$,则可对④进行判断.
解答 解:∵b=4a,
∴抛物线的对称轴为直线x=-$\frac{b}{2a}$=-2,
而抛物线与x轴有两个交点,且两交点的距离小于2,
x=-1时,a-b+c>0,
∴抛物线的开口向上,抛物线与y轴的交点在x轴上方,
∴a>0,c>0,所以①错误,②正确;
∵抛物线与x轴有两个交点,
∴△=b2-4ac>0,所以③错误;
而b=4a,
∴16a2-4ac>0,
∴a>$\frac{c}{4}$,
∵$\frac{\sqrt{{b}^{2}-4ac}}{a}$<2,
∴b2-4ac<4a2,
即16a2-4ac<4a2,
∴a<$\frac{c}{3}$所以④正确.
故答案为②④.
点评 本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.也考查了二次函数图象与系数的关系.

练习册系列答案
相关题目
16.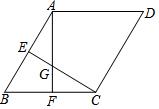 如图,在菱形ABCD中,∠B=60°,E、F分别是AB、BC的中点,CE、AF相交于点G,则四边形AGCD各边中点连线是( )
如图,在菱形ABCD中,∠B=60°,E、F分别是AB、BC的中点,CE、AF相交于点G,则四边形AGCD各边中点连线是( )
 如图,在菱形ABCD中,∠B=60°,E、F分别是AB、BC的中点,CE、AF相交于点G,则四边形AGCD各边中点连线是( )
如图,在菱形ABCD中,∠B=60°,E、F分别是AB、BC的中点,CE、AF相交于点G,则四边形AGCD各边中点连线是( )| A. | 平行四边形 | B. | 菱形 | C. | 矩形 | D. | 正方形 |
13.已知圆锥的底面半径为3cm,母线长为5cm,则圆锥的侧面积是( )
| A. | 20 cm2 | B. | 20π cm2 | C. | 15 cm2 | D. | 15π cm2 |
10.若最简二次根式$\sqrt{1+2a}$与2$\sqrt{3}$是同类二次根式,则a的值为( )
| A. | 1 | B. | -1 | C. | 2 | D. | $\frac{5}{2}$ |
17.计算(ab2)4的结果,正确的是( )
| A. | a4b8 | B. | a4b6 | C. | ab8 | D. | ab6 |
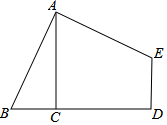 如图,AC⊥BD于C,∠D=90°,AB=AE且AB⊥AE,四边形ABDE的面积为36,则AC=6.
如图,AC⊥BD于C,∠D=90°,AB=AE且AB⊥AE,四边形ABDE的面积为36,则AC=6. 在图中,AHIJ,AEFG和ABCD是三个相似长方形,若AH,AE与AB的长度之比为1:3:5,求图中黄色区域与蓝色区域的面积之比.
在图中,AHIJ,AEFG和ABCD是三个相似长方形,若AH,AE与AB的长度之比为1:3:5,求图中黄色区域与蓝色区域的面积之比.